Cho tam giác đều ABC cạnh a. Gọi M là trung điểm của AB và N là hột điểm trên cạnh AC sao cho NC = 2 NA. a) Phân tích vecto MN theo hai vecto AB và AC. b) Gọi G là trọng tâm của tam giác ABC. Tinh CG.CAN theo a.

Những câu hỏi liên quan
Bài 1. Cho tam giác ABC , gọi M là điểm trên cạnh BC sao cho MC = 2MB
1) Phân tích vecto AM theo vecto AB, vecto AC
2) Gọi D là trung điểm của AC, phân tích vecto MD theo vecto BA, vecto BC
3) Gọi E là trung điểm của BD . Chứng minh A, E, M thẳng hàng
4) Phân tích vecto BC theo vecto BD, vecto AM
Cho tam giác ABC Gọi M là trung điểm của AB có G là trọng tâm,I là trung điểm của AB ,M thuộc AB sao cho vtMA+3vtMB=vt0.
a) Phân tích vecto MG theo hai vecto MC và MB.
Cho tam giác ABC. M, D lần lượt là trung điểm AB, BC. N trên cạnh AC sao cho CN = 2NA. Lấy K là trung điểm của MN. Phân tích vecto KD theo 2 vecto AB và AC.
\(\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AD}\)(D là trung điểm của BC) (1)
\(\overrightarrow{AM}+\overrightarrow{AN}=2\overrightarrow{AK}\)(K là trung điểm của MN) (2)
Lấy (1) trừ (2) có: \(\left(\overrightarrow{AB}+\overrightarrow{AC}\right)-\left(\overrightarrow{AM}+\overrightarrow{AN}\right)=2\left(\overrightarrow{AD}-\overrightarrow{AK}\right)\)
⇔\(\dfrac{\left(\overrightarrow{AB}+\overrightarrow{AC}\right)-\left(\overrightarrow{AM}+\overrightarrow{AN}\right)}{2}\)=\(\overrightarrow{KD}\)
⇔\(\dfrac{\left(\overrightarrow{AB}+\overrightarrow{AC}\right)-\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\right)}{2}\)=\(\overrightarrow{KD}\)
⇔\(\dfrac{\overrightarrow{AB}+\overrightarrow{AC}-\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{3}\overrightarrow{AC}}{2}\)=\(\overrightarrow{KD}\)
⇔\(\dfrac{\dfrac{1}{2}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}}{2}\)=\(\overrightarrow{KD}\)
⇔\(\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)=\(\overrightarrow{KD}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC. Gọi M, N, E lần lượt là trung điểm của AB, AC và BC. Gọi I là trung điểm của MN. Đặt vecto u vecto AB , vecto v vecto ACa) Hãy phân tích vecto AI theo hai vecto u và vb) Hãy phân tích vecto EI theo hai vecto u và v.
Đọc tiếp
Cho tam giác ABC. Gọi M, N, E lần lượt là trung điểm của AB, AC và BC. Gọi I là trung điểm của MN. Đặt vecto u = vecto AB , vecto v = vecto AC
a) Hãy phân tích vecto AI theo hai vecto u và v
b) Hãy phân tích vecto EI theo hai vecto u và v.
a: \(\overrightarrow{AI}=\dfrac{1}{2}\left(\overrightarrow{AM}+\overrightarrow{AN}\right)=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Gọi M, N là các điểm nằm trên các cạnh AB và CD sao cho AM AB, CN CD. Gọi G là trọng tâm của tam giác BMN. Hãy phân tích theo hai vecto .
Đọc tiếp
Cho hình bình hành ABCD. Gọi M, N là các điểm nằm trên các cạnh AB và CD sao cho AM = 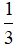
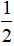
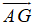
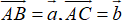
cho tam giác ABC . gọi M là điểm thuộc cạnh AB , N là điểm thuộc cạnh AC sao cho AM dfrac{1}{3} AB , AN dfrac{3}{4} AC . gọi O là giao điểm của CM và BN a) Biểu diễn vecto overrightarrow{AO} theo 2 vecto overrightarrow{AB} và overrightarrow{AC}b) trên đường thẳng BC lấy E . Đặt overrightarrow{BE} x.overrightarrow{BC} . tìm x để A,O ,E thẳng hàng
Đọc tiếp
cho tam giác ABC . gọi M là điểm thuộc cạnh AB , N là điểm thuộc cạnh AC sao cho AM =\(\dfrac{1}{3}\) AB , AN =\(\dfrac{3}{4}\) AC . gọi O là giao điểm của CM và BN
a) Biểu diễn vecto \(\overrightarrow{AO}\) theo 2 vecto \(\overrightarrow{AB}\) và \(\overrightarrow{AC}\)
b) trên đường thẳng BC lấy E . Đặt \(\overrightarrow{BE}\)= x.\(\overrightarrow{BC}\) . tìm x để A,O ,E thẳng hàng
Cho tam giác ABC có M là trung điểm AB, N là điểm trên cạnh AC sao cho AN = 2 NC. Gọi K là trung điểm MN. Hãy phân tích vectơ AK theo vectơ AB và vectơ AC.
Cho tam giác ABC , M là điểm trên cạnh BC sao cho 7MB = BC , N là trung điểm của cạnh AB . Đặt u → =BA → , v→ = BC →
a, phân tích vecto CN → theo 2 vecto u → và v →
b, phân tích vecto AM → theo 2 vecto u → và v →
a: \(\overrightarrow{CN}=\dfrac{1}{2}\overrightarrow{CA}+\dfrac{1}{2}\overrightarrow{CB}\)
\(=\dfrac{1}{2}\overrightarrow{CB}+\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{CB}\)
\(=\dfrac{1}{2}\overrightarrow{u}-\overrightarrow{v}\)
Đúng 1
Bình luận (0)
1.cho tam giác ABC gọi K là điểm đối xứng của trọng tâm G qua B.
a. Chứng minh KA-5KB +KC=0 ( đều là vecto hết )
b. Tính vecto AB và AC theo hai vecto AG và AK