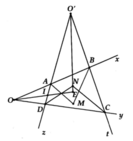
Hình bình hành ABCD có ∠ A = 120 ° , AB = a, BC = b. Các đường phân giác của bốn góc A, B, C, D cắt nhau tạo thành tứ giác MNPQ. Tính diện tích tứ giác MNPQ.

Những câu hỏi liên quan
Hình bình hành ABCD có \(\widehat{A}=120^0,AB=a,BC=b\). Các đường phân giác của bốn góc A, B, C, D cắt nhau tạo thành tứ giác MNPQ. Tính diện tích tứ giác MNPQ ?
Giải:
Ta có: \(\widehat{DAB}=120^0\left(gt\right)\) nên \(\widehat{ADC}=60^0\)
Đường phân giác của \(\widehat{A}\) cắt đường phân giác của \(\widehat{D}\) tại \(M\) thì \(\Delta ADM\) có hai góc bằng \(60^0\) và \(30^0\) nên các đường phân giác đó vuông góc với nhau.
Lập luận tương tự chứng tỏ tứ giác \(MNPQ\) có \(4\) góc vuông nên nó là hình chữ nhật.
Trong tam giác vuông \(ADM\) có:
\(DM=AD\sin\widehat{DAM}=b\sin60^0=\dfrac{b\sqrt{3}}{2}\)
Trong tam giác vuông \(DCN\) và có:
\(DN=DC\sin\widehat{DCN}=a\sin60^0=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow MN=DN-DM=\left(a-b\right)\dfrac{\sqrt{3}}{2}\)
Trong tam giác vuông \(DCN\) có \(CN=CD\cos60^0=\dfrac{a}{2}\)
Trong tam giác vuông \(BCP\) có \(CP=CB\cos60^0=\dfrac{b}{2}\)
Vậy \(NP=CN-CP=\dfrac{a-b}{2}\)
Suy ra diện tích hình chữ nhật \(MNPQ\) là:
\(MN.NP=\left(a-b\right)^2\dfrac{\sqrt{3}}{4}\left(đvdt\right)\)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có \(\widehat{A}=120\)độ , AB = a , BC = b , các đường phân giác của 4 góc cắt nhau tạo thành từ giác MNPQ . Tính diện tích tứ giác MNPQ .
Cho hình bình hành ABCD có AB= 6cm, BC= 4cm, góc B =60 độ. Ccác đường phân giác của các góc A,B,C,D cắt nhau tạo thành một tứ giác. C/m tứ giác vừa tạo là hình chữ nhật
Cho hình bình hành ABCD, AB = 6cm, AD = 4cm. Các tia phân giác của các góc A, B, C, D cắt nhau tạo thành tứ giác EFGH.
a) Tứ giác EFGH là hình gì ?
b ) Tính độ dài đường chéo của tứ giác EFGH
c ) Hinh bình hành ABCD có thêm điều kiện gì để diện tích tứ giác EFGH lớn nhất ?
Cho hai góc nhọn
x
O
y
^
và
z
O
t
^
có các cạnh cắt nhau tạo thành hình ABCD như hình vẽ. Xét hình ABCD.a) Chứng minh tổng bốn góc A + B + C + D bằng
360
°
.
b) Cho biết
A
^
130
°...
Đọc tiếp
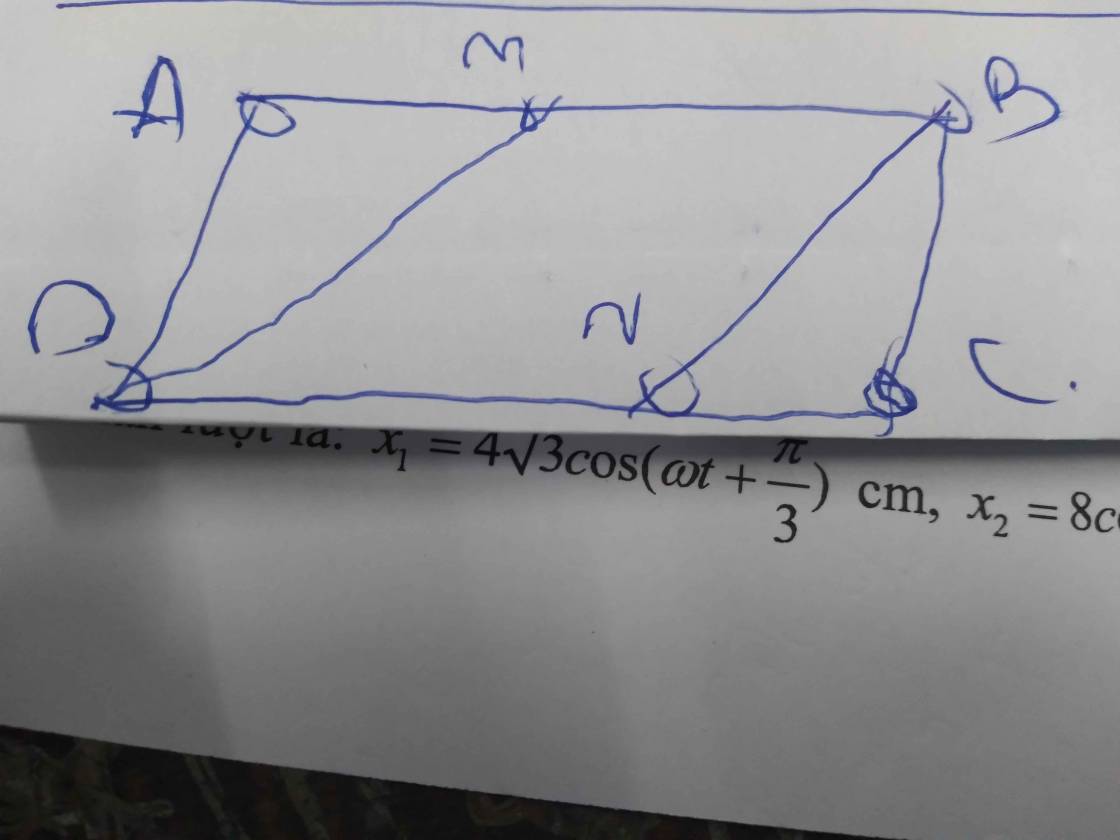
Cho hai góc nhọn x O y ^ và z O ' t ^ có các cạnh cắt nhau tạo thành hình ABCD như hình vẽ. Xét hình ABCD.
a) Chứng minh tổng bốn góc A + B + C + D bằng 360 ° .
b) Cho biết A ^ = 130 ° , B ^ = 120 ° , C ^ = 50 ° .Các tia phân giác của A ^ , B ^ cắt nhau tại M, các tia phân giác của D ^ , C ^ cắt nhau tại N. Tính A M B ^ , D N C ^ .
c) Chứng minh tia phân giác của hai góc x O y ^ và z O ' t ^ vuông góc với nhau.
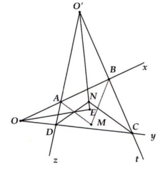
Bài 2: cho hình bình hành ABCD có AB>BC, phân giác của góc D cắt AB tại M,phân giác của góc B cắt CD tại N.c/m
a,AM=CN
b,tứ giác DMBN là hình bình hành
Cho hình bình hành ABCD các tia phân giác của các góc của hình bình hành cắt nhau tạo thành tứ giác EFGH. CMR:
a, Tứ giác EFGH là hình gì? Vì sao?
b, EG = FH và bằng hiệu giữa hai cạnh kề của hình bình hành ABCD
c, Hình bình hành ABCD cần điều kiện gì để EFGH là hình vuông?
Cho hình bình hành ABCD. Các tia phân giác của các góc của hình bình hành cắt nhau tạo thành tứ giác EFGH.
a) Tứ giác EFGH là hình gì ? Vì sao ?
b) Chứng minh rằng EG = FH và bằng hiệu giữa hai cạnh kề một đỉnh của hình bình hành ABCD.
c) Hình bình hành ABCD cần có thêm điều kiện gì để EFGH là hình vuông?
câu 1 cho tam giác ABC vuông tại A đường cao AH gọi M và N là hình chiếu của H trên AB và AC
a)cm AH=MN
b)gọi ILK lần lượt là các điểm đối xứng với H qua AB và AC . Cm I,L,K thẳng hàng
câu 2 cho hình bình hành ABCD các đường phân giác của góc A ,góc B , góc C ,góc D cắt nhau tạo thành tứ giác MNPQ .Cm tứ giác MNPQ là hình gì ?vì sao?
a)xét tứ giác AMNH có:
góc HMA= 90 độ
góc HNA = 90 độ
góc MAH= 90 độ ( tam giác ABC vuông tại A)
=> AMHN là hình chữ nhật
=> AH=MN( tính chất 2 đường chéo)
tứ giác AMHN có \(\widehat{A}\)=\(\widehat{M}\)=\(\widehat{N}\)=90\(^o\)
nên AMHN là hcn => AH=MN