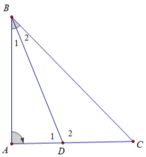
+) Xét tam giác BDC có ∠D1 là góc ngoài tam giác tại đỉnh D nên:

∠D1 = ∠B2 + ∠C

Suy ra: ∠D1 > ∠B2 (góc ngoài của ΔBDC)

Mà ∠B1 = ∠B2 ( vì BD là tia phân giác của góc ABC ) nên ∠D1 > ∠B1 .

ΔABD có ∠D1 > ∠B1 nên AB > AD.

a: AC=căn 10^2-6^2=8cm

AB<AC<BC

=>góc C<góc B<góc A

b: Xét ΔBAD vuông tại A và ΔBED vuông tại E có

BD chung

góc ABD=góc EBD

=>ΔBAD=ΔBED

=>BA=BE và DA=DE

=>BD là trung trực của AE

a) Xét tam giác ABD và EBD có:

BA = BE (gt)

\(\widehat{ABD}=\widehat{EBD}\) (Do BD là tia phân giác góc B)

BD chung

\(\Rightarrow\Delta ABD=\Delta EBD\left(c-g-c\right)\)

\(\Rightarrow AD=ED\) (Hai cạnh tương ứng)

b)  Do \(\Delta ABD=\Delta EBD\left(cmt\right)\Rightarrow\widehat{BED}=\widehat{BAD}=90^o\)

Xét tam giác vuông ABC ta có \(\widehat{ABC}=90^o-\widehat{ACB}\)

Xét tam giác vuông DEC ta có \(\widehat{EDC}=90^o-\widehat{ACB}\)

Vậy nên \(\widehat{EDC}=\widehat{ABC}\)

c) Gọi giao điểm của AE và BD là I.

Xét tam giác ABI và tam giác EBI có:

AB = EB (gt)

\(\widehat{ABI}=\widehat{EBI}\)

BD chung

\(\Rightarrow\Delta ABI=\Delta EBI\left(c-g-c\right)\)

\(\Rightarrow\widehat{AIB}=\widehat{EIB}\) (Hai góc tương ứng)

Mà chúng lại ở vị trí kề bù nên \(\widehat{AIB}=\widehat{EIB}=90^o\)

Vậy nên \(AE\perp BD\)

Câu hỏi là j vậy bn ?

what the hell??????

Bài 5: Cho tam giác ABC có ba góc nhọn, AB<AC. Kẻ BD vuông góc với AC tại D, CE vuông góc với AB tại E. Gọi H là giao điểm của BD và CE. So sánh độ dài HB và HC.

Bài 6: Cho tam giác ABC có AB<AC. Tia phân giác của góc B và C cắt nhau tại I. Từ I vẽ IH vuông góc với BC. So sánh độ dài HB và HC.

~~~Đây,các bạn giúp mk vs~~~

Bài 5: Cho tam giác ABC có ba góc nhọn, AB<AC. Kẻ BD vuông góc với AC tại D, CE vuông góc với AB tại E. Gọi H là giao điểm của BD và CE. So sánh độ dài HB và HC.

Bài 6: Cho tam giác ABC có AB<AC. Tia phân giác của góc B và C cắt nhau tại I. Từ I vẽ IH vuông góc với BC. So sánh độ dài HB và HC.

Bạn viết đề bài cho đầy đủ chứ -.-

~ Vào thông kê của bạn ý là thấy đề ~

Bài 5: 

Bài làm

Xét tam giác ABC có:

AB < AC (gt)

=> \(\widehat{ABC}>\widehat{ACB}\)( Quan hệ giữa góc và cạnh đối diện )                    (1)

Xét tam giác EBC vuông ở E có:

\(\widehat{ABC}+\widehat{ECB}=90^0\)                           (2)

Xét tam giác DBC vuông ở D có:

\(\widehat{ACB}+\widehat{DBC}=90^0\)                        (3)

Từ (1) , (2) và (3) => \(\widehat{ECB}< \widehat{DBC}\)

Xét tam giác HBC có: 

\(\widehat{ECB}< \widehat{DBC}\)       ( theo quan hệ giữa góc và cạnh đối diện có )

BH < HC 

Vậy BH < HC 

Bài 6

Bài làm:

Xét tam giác ABC có:

AB < AC ( gt )

\(\widehat{ABC}>\widehat{ACB}\)( quan hệ giữa góc và cạnh đối diện )                     (1)

Mà BI là phân giác góc ABC 

=> \(\frac{1}{2}\widehat{ABC}=\widehat{ABI}=\widehat{IBC}\)                                         (2)

Và CI là phân giác góc ACB

=> \(\frac{1}{2}\widehat{ACB}=\widehat{ACI}=\widehat{ICB}\)                                      (3)

Từ (1), (2) và (3) => \(\widehat{ABI}=\widehat{IBC}>\widehat{ACI}=\widehat{ICB}\)              (4)

Xét tam giác IHB vuông ở H có:

\(\widehat{IBC}+\widehat{BIH}=90^0\)                      (5)

Xét tam giác IHC vuông ở H có:

\(\widehat{ICB}+\widehat{CIH}=90^0\)                 (6)

Từ (4), (5) và (6) => \(\widehat{BIH}< \widehat{CIH}\)

Xét tam giác IBC có:

\(\widehat{BIH}< \widehat{CIH}\)( Theo quan hệ giữa góc đối và cạnh đối diện có: )

BH < HC 

Vậy BH < HC

# Học tốt #

a) Xét tam gics BAD và BED ta có:

BD là cạnh chung (gt)

AB=AE (gt)

Góc ABD=góc DBC ( vid BD là phân giác của gốc B)

=> Tam giác BAD=tam gics BED (c.g.c)

=>AD=DE ( 2 cạnh tương ứng)

=> Tam giác BAD= tam giác BED

=> góc BAD=BED(2 góc tương ứng)

=>BED=BAD=90*

Xét tam giác ABC và EDC ta cosL'

BAC=DEC=90*

góc C chung

=> tam giác ABC~tam giác EDC (g-g)

=> goác ABC=EDC

b) Xét tam giác ABE ta có:

AB=BE

=> tam giác ABE cân tại B

mà BD là tia phân giác của góc B

=> BD là đường cao

=> BD vuông góc vs AE

g-g là j

phần 2 câu a bạn sai rồi 

Giải 

có góc abc + góc c =90⁰(tam giác abc vuông tại a)

Mà góc edc + góc c =90⁰(tam giác edc vuông tại d)

Vậy góc abc = góc edc 

*Tự vẽ hình

a) Xét tam giác ABD và EBD có :

\(\widehat{ABD}=\widehat{DBE}\left(gt\right)\)

BD : cạnh chung

BA=BE(gt)

=> Tam giác ABD=EBD(c.g.c)

=> AD=DE

và \(\widehat{BAD}=\widehat{DEB}=90^o\)

\(\Rightarrow\widehat{BAD}=\widehat{DEC}=90^o\)

b) Gọi giao điểm của BD và AE là O

Tam giác ABO=EBO(c.g.c) (tự cm)

=> \(\widehat{BOA}=\widehat{BOE}\)

Mà : \(\widehat{BOA}+\widehat{BOE}=180^o\)

\(\Rightarrow\widehat{BOA}=90^o\)

\(\Rightarrow AE\perp BD\left(đccm\right)\)

#H

a: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có

BD chung

góc ABD=góc HBD

=>ΔBAD=ΔBHD

=>DA=DH

b: AD=DH

DH<DC

=>AD<DC

c: Xét ΔBKC có

KH,CA là đường cao

KH cắt CA tại D

=>D là trực tâm

=>BD vuông góc KC