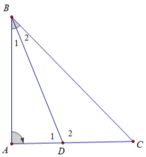
+) Xét tam giác BDC có ∠D1 là góc ngoài tam giác tại đỉnh D nên:
∠D1 = ∠B2 + ∠C
Suy ra: ∠D1 > ∠B2 (góc ngoài của ΔBDC)
Mà ∠B1 = ∠B2 ( vì BD là tia phân giác của góc ABC ) nên ∠D1 > ∠B1 .
ΔABD có ∠D1 > ∠B1 nên AB > AD.
Cho tam giác ABC vuông góc tại A, phân giác BD. So sánh các độ dài BC và BD.
Cho tam giác ABC vuông tại A có AB <AC, góc C = 30 độ,BD là tia phân giác của góc ABC (D thuộc AC)
a) So sánh BD và AB
b) Trên tia đối của tia AB lây điểm E sao cho AE = AB chứng minh tam giác CAE= tam giác CAB
c) So sánh AD và CD
d) Đường thẳng BD cắt đường thẳng EC tại F, gọi I là trung điểm của BC chứng minh ba điểm E,D ,I thẳng hàng
Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt AC tại D. So sánh độ dài AB và AD?
Cho tam giác ABC vuông tại A , Tia phân giác của góc ABC cắt AC tại điểm D . Từ D kẻ vuông góc với BC tại điểm H
a, chứng minh AD = DH
b, so sánh độ dài AD và DC
c, gọi K là giao điểm của AB và DH
BD là đường trung trực của đoạn thẳng KC
Giải giúp mình phần c với ạ 28 tháng tư cần rồi ạ
Bài :Cho tam giác ABC vuông tại A. Tia phân giác của góc ABC cắt AC tại D. Từ D kẻ DH vuông góc với BC tại H và DH cắt AB tại K. a. Chứng minh: AD = HD b. So sánh độ dài cạnh AD và DC c. Chứng minh tam giác KBC là tam giác cân.
cho tam giác ABC có góc = 90 độ Tia phân giác BD của góc D Trên cạnh BC lấy điểm E sao BE=BA
a)so sánh độ dài các đoạn AD và DE so sánh góc EDC và ABC
b)chứng minh AE vuông góc AD
Bài 5: Cho tam giác ABC có ba góc nhọn, AB<AC. Kẻ BD vuông góc với AC tại D, CE vuông góc với AB tại E. Gọi H là giao điểm của BD và CE. So sánh độ dài HB và HC.
Bài 6: Cho tam giác ABC có AB<AC. Tia phân giác của góc B và C cắt nhau tại I. Từ I vẽ IH vuông góc với BC. So sánh độ dài HB và HC.
Bài 5: Cho tam giác ABC có ba góc nhọn, AB<AC. Kẻ BD vuông góc với AC tại D, CE vuông góc với AB tại E. Gọi H là giao điểm của BD và CE. So sánh độ dài HB và HC.
Bài 6: Cho tam giác ABC có AB<AC. Tia phân giác của góc B và C cắt nhau tại I. Từ I vẽ IH vuông góc với BC. So sánh độ dài HB và HC.
Cho tam giác ABC vuông tại A , tia phân giác BD của góc B ( \(D\in AC\)) . Lấy điểm E trên cạnh BC sao cho BE = BA .
a) So sánh độ dài các đoạn AD và DE .
b) So sánh góc EDC và góc ABC .
c) Chứng minh : AE vuông góc với BD .
