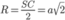Cho hình chóp S . A B C có S A ⊥ ( A B C ) , S A = a 3 . Tam giác ABC vuông cân tại B, A C = 2 a . Thể tích khối chóp S . A B C bằng.
A. a 3 3
B. a 3 3 6
C. 2 a 3 3 2
D. a 3 3 3
Kẻ \(BK\perp AC\Rightarrow BK\perp\left(SAC\right)\)
\(\Rightarrow BK=d\left(B;\left(SAC\right)\right)\)
\(\dfrac{1}{BK^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Rightarrow BK=\dfrac{AB.AC}{\sqrt{AB^2+AC^2}}=\dfrac{a\sqrt{3}}{2}\)
Kẻ \(CP\perp BH\Rightarrow CP\perp\left(SBH\right)\)
\(\Rightarrow CP=d\left(C;\left(SBH\right)\right)\)
\(\widehat{CBP}=\widehat{ACB}=30^0\Rightarrow CH=BC.sin30^0=\dfrac{a\sqrt{3}}{2}\)
\(BH=\dfrac{AC}{2}=\dfrac{1}{2}\sqrt{AB^2+AC^2}=a\)\(\Rightarrow SH=\sqrt{SB^2-BH^2}=a\)
Kẻ \(HE\perp BC\) , kẻ \(HF\perp SE\Rightarrow HF=d\left(H;\left(SBC\right)\right)\)
\(HE=CH.sin30^0=\dfrac{a}{2}\)
\(\dfrac{1}{HF^2}=\dfrac{1}{SH^2}+\dfrac{1}{HE^2}\Rightarrow HF=\dfrac{SH.HE}{\sqrt{SH^2+HE^2}}=\dfrac{a\sqrt{5}}{5}\)
Cho hình chóp .S ABCD có đáy ABCD là hình bình hành thỏa mãn AB=a, AC=a 3 . Biết tam giác SBC cân tại S, tam giác SCD vuông tại C và khoảng cách từ D đến mặt phẳng (SBC) bằng a 3 3 . Tính thể tích V của khối chóp đã cho
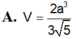
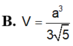
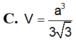
Cho hình chóp S. ABC có đáy là tam giác ABC đều cạnh a, tam giác SBA vuông tại B, tam giác SAC vuông tại C. Biết góc giữa hai mặt phẳng (SAB) và (ABC) bằng 60 o . Tính thể tích khối chóp S.ABC theo a.
A. 3 a 3 8
B. 3 a 3 12
C. 3 a 3 6
D. 3 a 3 4
Chọn B
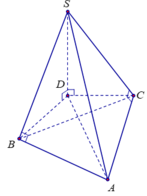
Gọi D là hình chiếu của S lên mặt phẳng (ABC), suy ra S D ⊥ A B C .
Ta có S D ⊥ A B và S B ⊥ A B ( g t ) , suy ra A B ⊥ S B D ⇒ B A ⊥ B D .
Tương tự có A C ⊥ D C hay tam giác ACD vuông ở C.
Dễ thấy ∆ S B A = ∆ S C A (cạnh huyền và cạnh góc vuông), suy ra SB=SC. Từ đó ta chứng minh được ∆ S B D = ∆ S C D nên cũng có DB=DC.
Vậy DA là đường trung trực của BC, nên cũng là đường phân giác của góc B A C ^ .
Ta có
D
A
C
^
=
30
o
, suy ra
D
C
=
a
3
. Ngoài ra góc giữa hai mặt phẳng (SAB) và (ABC) là
S
B
D
^
=
60
o
suy ra
tan
S
B
D
^
=
S
D
B
D
⇒
S
D
=
B
D
tan
S
B
D
^
=
a
3
.
3
=
a
Vậy
V
S
.
A
B
C
=
1
3
.
S
∆
A
B
C
.
S
D
=
1
3
a
2
3
4
.
a
=
a
3
3
12
Cho hình chóp S.ABCD có đáy là hình thang cân, S A ⊥ A B C D , A D = 2 B C = 2 A B . Trong tất cả các tam giác mà 3 đỉnh lấy từ 5 điểm S, A, B, C, D có bao nhiêu tam giác vuông?
A. 3
B. 6
C. 5
D. 7
Cho hình chóp S.ABCD có đáy là hình thang cân, S A ⊥ A B C D , A D = 2 B C = 2 A B . Trong tất cả các tam giác mà 3 đỉnh lấy từ 5 điểm S, A, B, C, D có bao nhiêu tam giác vuông?
A. 3
B. 6
C. 5
D. 7
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, đỉnh S cách đều các điểm A,B,C. Biết AC = 2a,BC = a; góc giữa đường thẳng SB và mặt đáy (ABC) bằng 60 o . Tính theo a thể tích V của khối chóp S.ABC?
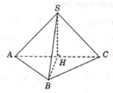
A. V = a 6 3 4 .
B. V = a 6 3 6 .
C. V = a 3 2 .
D. V = a 6 3 12 .
Đáp án C.
Hướng dẫn giải: Gọi H là trung điểm AC.
Do tam giác ABC vuông tại B nên H là tâm đường tròn ngoại tiếp tam giác ABC.
Đỉnh S cách đều các điểm A, B,C nên hình chiếu của S trên mặt đáy (ABC) trùng với tâm đường tròn ngoại tiếp tam giác ABC
suy ra S H ⊥ ( A B C )
![]()
Tam giác vuông SBH, có
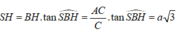
Tam giác vuông ABC ,
có A B = A C 2 - B C 2 = a 3
Diện tích tam giác vuông
S ∆ A B C = 1 2 B A . B C = a 3 2 2
Vậy V S . A B C = 1 3 S ∆ A B C . S H = a 3 2
Cho hình chóp S.ABC có SA=2a, SA ⊥ (ABC), tam giác ABC vuông tại B và AB=a. Khoảng cách từ điểm A đến mặt phẳng (SBC) là
Kẻ đường cao AH của \(\Delta SAB\)
Ta có: SA\(\perp\)( ABC ) = > SA\(\perp\)BC
mà AB \(\perp\)BC ( tam giác ABC vuông tại B )
=> BC \(\perp\)(SAB ) => BC \(\perp\)AH lại có: AH \(\perp\)SB ( theo cách vẽ đường cao)
=> AH \(\perp\)(SBC )
=> d ( A; (SBC )) = AH
Xét \(\Delta\)SAB vuông tại A có AH là đường cao
=> \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{SA^2}=\frac{1}{a^2}+\frac{1}{4a^2}=\frac{5}{4a^2}\Rightarrow AH=\frac{2\sqrt{5}}{5}\)
Vậy d ( A; (SBC )) = AH = \(\frac{2\sqrt{5}}{5}\)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật cạnh a, S A ⊥ (A B C D) ,SC tạo với mặt đáy một góc 60 độ và (SAB ) một góc a với sin a = căn 3/ 4 . Tính chiều cao khối chóp.
Đáy là hình vuông hay chữ nhật bạn? Hình chữ nhật sao có các cạnh bằng nhau và bằng a được?
Cho hình chóp tam giác đều S.ABC có AC = SC = 8 cm , SH = 6,93 cm ,S tam giác ABC = 27,72 cm2
a) Cho biết độ dài trung đoạn của hình chóp S.ABC.
b) Tính diện tích xung quanh và diện tích toàn phần của hình chóp S.ABC.
c) Tính thể tích của hình chóp tam giác đều S.ABC biết chiều cao của hình chóp là 7,5 cm
a) Độ dài trung đoạn của hình chóp S.ABC là độ dài đoạn thẳng từ trung điểm của cạnh đáy đến đỉnh của hình chóp. Vì tam giác ABC là tam giác đều, nên ta có thể tính độ dài trung đoạn bằng cách sử dụng công thức Pythagoras: Trung đoạn = căn bậc hai của (AC^2 - (AC/2)^2) = căn bậc hai của (8^2 - (8/2)^2) = căn bậc hai của (64 - 16) = căn bậc hai của 48 = 4 căn 3 cm
b) Diện tích xung quanh của hình chóp S.ABC là tổng diện tích các mặt bên của hình chóp. Vì tam giác ABC là tam giác đều, nên diện tích mặt bên của hình chóp là diện tích tam giác đều. Ta có công thức tính diện tích tam giác đều: Diện tích tam giác đều = (cạnh^2 * căn 3) / 4 = (8^2 * căn 3) / 4 = 16 căn 3 cm^2
Diện tích xung quanh = Diện tích tam giác đều + Diện tích đáy = 16 căn 3 + 27,72 = 16 căn 3 + 27,72 cm^2
Diện tích toàn phần của hình chóp là tổng diện tích xung quanh và diện tích đáy: Diện tích toàn phần = Diện tích xung quanh + Diện tích đáy = 16 căn 3 + 27,72 + 27,72 = 16 căn 3 + 55,44 cm^2
c) Thể tích của hình chóp tam giác đều S.ABC được tính bằng công thức: Thể tích = (Diện tích đáy * Chiều cao) / 3 = (27,72 * 7,5) / 3 = 69,3 cm^3
Cho hình chóp .S ABC có SA vuông góc mặt phẳng (ABC) tam giác ABC vuông tại .B Biết SA= 2a, AB= a, BC= a 3 .Tính bán kính R của mặt cầu ngoại tiếp hình chóp đã cho
A. a
B. 2a
C. a 2
D. 2a 2
Đáp án C
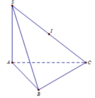
Gọi I là trung điểm của SC.
Khi đó I là tâm mặt cầu ngoại tiếp hình chóp
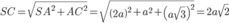 Bán kính
Bán kính