Biết rằng hàm số y = sin 2 x + b cos 2 x - x ( 0 < x < π ) đạt cực trị tại các điểm x = π 6 và x = π 2 Tính giá trị của biểu thức T = a-b
A. 3 + 1 2
B. 3 - 1 2
C. 3 - 1
D. 3 + 1
Biết rằng hàm số y = sin2x + b.cosx - x ( 0 < x < π ) đạt cực trị tại các điểm x = π 6 và x = π 2 Tính giá trị của biểu thức T = a - b
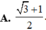
![]()
![]()
![]()
Cho \(f\left(x\right)=\frac{2}{3}x^3+\left(\cos a-3\sin a\right)x^2-8\left(1+\cos a\right)x+1\)
a) Chứng minh rằng hàm số luôn có cực đại và cực tiểu
b) Giả sử hàm số đạt cực trị tại \(x_1,x_2\). Chứng minh rằng \(x_1^2+x_2^2\le18\)
a) Xét phương trình : \(f'\left(x\right)=2x^2+2\left(\cos a-3\sin a\right)x-8\left(1+\cos2a\right)=0\)
Ta có : \(\Delta'=\left(\cos a-3\sin a\right)^2+16\left(1+\cos2a\right)=\left(\cos a-3\sin a\right)^2+32\cos^2\), \(a\ge0\) với mọi a
Nếu \(\Delta'=0\Leftrightarrow\cos a-3\sin a=\cos a=0\Leftrightarrow\sin a=\cos a\Rightarrow\sin^2a+\cos^2a=0\) (Vô lí)
Vậy \(\Delta'>0\)
với mọi a \(\Rightarrow f'\left(x\right)=0\)
có 2 nghiệm phân biệt \(x_1,x_2\) và hàm số có cực đại, cực tiểu
b) Theo Viet ta có \(x_1+x_2=3\sin a-\cos a\)
\(x_1x_2=-4\left(1+\cos2a\right)\)
\(x^2_1+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=\left(3\sin a-\cos a\right)^2+8\left(1+\cos2a\right)=9+8\cos^2a-6\sin a\cos a\)
\(=9+9\left(\sin^2a+\cos^2a\right)-\left(3\sin a+\cos a\right)^2=18-\left(3\sin a+\cos2a\right)\le18\)
Hàm số y = a sin 2 x + b cos 3 x - 2 x ( 0 < x < 2 π ) đạt cực trị tại x = π 2 ; x = π . Khi đó, giá trị của biểu thức P = a + 3 b - 3 a b là:
A. 3
B. -1
C. 1
D. -3
Chọn C
![]()
![]()
Hàm số đạt cực trị tại x = π 2 ; x = π nên ta có hệ phương trình
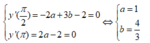
Do đó, giá trị của biểu thức P = a + 3 b - 3 a b =1
Giá trị lớn nhất của hàm số f(x) = sin x + cos 2x trên [0; π ] là
A. 5 4
B. 1
C. 2
D. 9 8
Có bao nhiêu mệnh đề đúng trong các phát biểu sau?
1. Hàm số không có đạo hàm tại x = 0.
2. Hàm số không liên tục tại x = 0.
3. Hàm số không có cực trị tại x = 0.
4. Hàm số đạt cực trị tại x = 0.
A. 0
B. 1
C. 2
D. 3
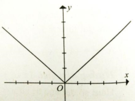
Đồ thị hàm số y = |x| có dạng hình vẽ.
Từ đồ thị trong hình ta có hàm số y = |x| liên tục tại x = 0 nhưng không có đạo hàm tại điểm đó. Sử dụng định nghĩa cực trị ta có hàm số y = |x| đạt cực tiểu tại x = 0
Do đó mệnh đề 1 và 4 đúng. Chọn đáp án C
Cho hàm số y = 1 3 sin 3 x + m sin x Tìm tất cả các giá trị của m để hàm số đạt cực đại tại điểm x = π/3
A. m > 0
B. m = 0
C. m = 1/2
D. m = 2
Đáp án D.
Ta có: y’ = cos 3x + mcos x
Hàm số đạt cực đại tại
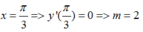
m = 2 => y’ = cos 3x + 2cos x => y’’ = -3sin 3x – 2sin x
=>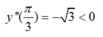
Vậy, m = 2
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f' (x) như hình vẽ bên. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:

1. Hàm số g(x) có 3 điểm cực trị.
2. Hàm số g(x)đạt cực tiểu tại x = 0.
3. Hàm số g(x)đạt cực đại tại x = 2.
4. Hàm số g(x)đồng biến trên khoảng (-2;0).
5. Hàm số g(x)nghịch biến trên khoảng (-1;1).
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 1.
B. 4.
C. 3.
D. 2.
1,Tìm tất cả các giá trị của m để hàm số y=2x^2 - 3mx + m - 2 trên x-1 đạt cực đại tại điểm x=2. 2, Tìm tất cả các giá trị của m để hàm số y= x^2 + mx +1 trên x+m đạt cực tiểu tại điểm x=2. 3, Tìm tất cả các giá trị của m để hàm số y=x^2 -(2m-1)x+3 trên x+2 có cực đại và cực tiểu . 4, Tìm m để hso y=x^2 +m(m^2-1)x-m^4+1 trên x-m có cực đại và cực tiểu. Mọi người giúp em với ạ . Em cảm ơn ạ !
Hàm số y = a sin x + b cos x + x + a + b 3 (với x ∈ 0 ; 2 π ) đạt cực trị tại x = π 3 ; x = π . Tính tổng a + b 3
A. 3
B. 3 - 1
C. 4
D. 3 + 1
Ta có y ' = a cos x + b sin x + 1 .
Do hàm số đạt cực trị tại các điểm x = π 3 ; x = π nên
y ' π 3 = 0 y ' π = 0 ⇔ 1 2 a - 3 2 b + 1 = 0 - a + 1 = 0 ⇔ a = 1 b = 3
Do đó a + b 3 = 4
Đáp án C