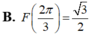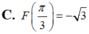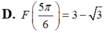Biết I = ∫ 0 π 2 x + x cos x − sin 3 x 1 + cos x d x = π 2 a − b c . Trong đó a, b, c là các số nguyên dương, phân số b c tối giản. Tính T = a 2 + b 2 + c 2
A. T = 16
B. T = 59
C. T = 69
D. T = 50
Cho hàm số y=f(x) liên tục trên đoạn [0;π/3].Biết f’(x).cosx+f(x).sinx=1, x ϵ [0;π/3] và f(0)=1. Tính tích phân I = ∫ 0 π 3 f x d x
A. 1/2 + π/3
B. 3 + 1 2
C. 3 - 1 2
D. 1/2
Cho hàm số f(x) có đạo hàm liên tục trên 0 ; π . Biết f 0 = 2 e và f(x) luôn thỏa mãn đẳng thức f ' x + sinx . f x = cosx . e cosx , ∀ x ∈ 0 ; π . Tính I = ∫ 0 π f x dx (làm tròn đến phần trăm).
A. I ≈ 6,55
B. I ≈ 17,30
C. I ≈ 10,31
D. I ≈ 16,91
Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?
a) {y = x + sinx, y = x với 0 ≤ x ≤ π } và {y = x + sinx, y = x với π ≤ x ≤ 2 π }
b) {y = sinx, y = 0 với 0 ≤ x ≤ π } và {y = cosx, y = 0 với 0 ≤ x ≤ π };
c) {y = x , y = x 2 }
và { y = 1 - x 2 , y = 1 − x}
Tính thể tích vật thể giới hạn bởi hai mặt phẳng x = 0 , x = π . Biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với Ox tại điểm có hoành độ x 0 ≤ x ≤ π là một tam giác vuông cân có cạnh huyền bằng sin x + 2 .
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Tính:F=Cos(π/4+α) x cos(π/4-α)
G=Sin(π/3+α) x cos(π/3-α)
H=cos(π/2-α) x sin(π/2+α)
I=sin(π/4+α) - cos(π/4-α)
K=cos(π/6-x) - sin(π/3+x)
Câu 1 : Tính thể tích vật thể tròn xoay khi quay hình phẳng (H) giới hạn bởi các đường y = x3 , y = 0, x=0, x=1 quanh trục hoành
Câu 2 : Biết F(x) là một nguyên hàm của hàm f(x) = sin2x và F(π/4) = 1. Tính F(π/6)
1.
\(V=\pi\int\limits^1_0x^6dx=\dfrac{\pi x^7}{7}|^1_0=\dfrac{\pi}{7}\)
2.
\(F\left(x\right)=\int sin2xdx=-\dfrac{1}{2}cos2x+C\)
\(f\left(\dfrac{\pi}{4}\right)=1\Leftrightarrow-\dfrac{1}{2}cos\dfrac{\pi}{2}+C=1\Rightarrow C=1\)
\(\Rightarrow F\left(x\right)=-\dfrac{1}{2}cos2x+1\Rightarrow F\left(\dfrac{\pi}{6}\right)=\dfrac{3}{4}\)
Tính thể tích của vật thể giới hạn bởi hai mặt phẳng x = 0 ; x = π Biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với Ox tại điểm có hoành độ x ( 0 ≤ x ≤ π ) là một tam giác vuông cân có cạnh huyền bằng sinx+2
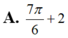
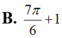
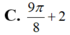
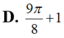
Biết F(x) là một nguyên hàm của hàm số f(x)=sin2 x+cosx. Giá trị F(π/2)-F(0) bằng
A. 2.
B. 1
C. -1
D. 4.
Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?
a) {y = x + sinx, y = x với 0 ≤ x ≤ π} và {y = x + sinx, y = x với π ≤ x ≤ 2π}
b) {y = sinx, y = 0 với 0 ≤ x ≤ π} và {y = cosx, y = 0 với 0 ≤ x ≤ π};
c) {y = √x, y = x 2 }
và { 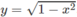 , y = 1 − x}
, y = 1 − x}
Cho hàm số F(x) là một nguyên hàm của hàm số f ( x ) = 2 cos x - 1 sin 2 x trên khoảng 0 ; π . Biết rằng giá trị lớn nhất của F(x) trên khoảng 0 ; π là 3 . Chọn mệnh đề đúng trong các mệnh đề sau?