Hàm số nào sau đây đồng biến trên R
A. y = x 3 − x 2 + 2 x + 3.
B. y = x 3 − x 2 − 3 x + 1.
C. y = 1 4 x 4 + x 2 − 2.
D. y = x − 1 x − 2 .
Cho hàm số y = f ( x ) liên tục trên R và có đạo hàm f ' ( x ) = ( 1 - x ) 2 ( x + 1 ) 3 ( 3 - x ) . Hàm số y = f ( x ) đồng biến trên khoảng nào dưới đây
![]()
![]()
![]()
![]()
trong các hàm số sau hàm số nào đồng biến trên R: A. y= 2x-1/x+2 B. y= -x^3+x^2-5x C. y= x^3+2x+1 D.-x^4-2x^2+3
\(\left(\frac{2x-1}{x+2}\right)'=\frac{5}{\left(x+2\right)^2}>0\)
Vậy hàm số \(y=\frac{2x-1}{x+2}\) đồng biến trên R. Chọn A.
A. là hàm phân thức bậc nhất trên bậc nhất nên không đồng biến trên \(ℝ\).
B., D. là đa thức, có hệ số cao nhất âm nên cũng không thể đồng biến trên \(ℝ\).
C>: \(\left(x^3+2x+1\right)'=3x^2+2>0,\forall x\inℝ\).
Ta chọn C.
Với giá trị nào của k thì:
a) Hàm số \(y=\dfrac{k^2+2}{k-3}x+\dfrac{1}{4}\)là hàm số đồng biến trên R?
b) Hàm số \(y=\dfrac{k+\sqrt{2}}{k^2+\sqrt{3}}x-\dfrac{3}{4}\)là hàm số nghịch biến trên R?
a) Hàm số đồng biến nếu \(\dfrac{k^2+2}{k-3}>0\) \(\Leftrightarrow k>3\)
b) Hàm số nghịch biến nếu \(\dfrac{k+\sqrt{2}}{k^2+\sqrt{3}}< 0\Leftrightarrow k< -\sqrt{2}\)
Cho hàm số y= f( x) có đạo hàm liên tục trên R. Đồ thị hàm số y= f’(x) như hình bên dưới
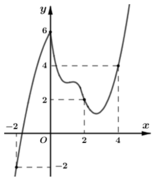
Hàm số g(x) = 2 . f(x) – x2 đồng biến trên khoảng nào trong các khoảng sau đây?
A. ( - ∞ ; - 2 )
B. (-2; 2)
C. (2; 4)
D. ( 2 ; + ∞ )
Cho hàm số y = f(x) xác định trên R, có bảng biến thiên sau
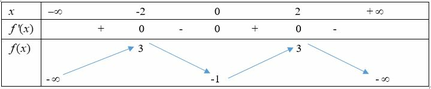
Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?
A. (0;2)
B. (-1;3)
C. (- ∞ ;3)
D. (- ∞ ;0)
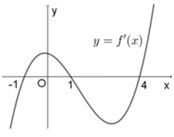
Cho hàm số y = f(x) có đạo hàm trên R và có đồ thị hàm số y = f'(x) như hình bên. Hàm số y= f (3-x) đồng biến trên khoảng nào dưới đây?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
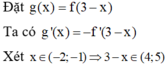
![]()
=> hàm số y=g(x) nghịch biến trên (-2; -1)
![]()
![]()
=>hàm số y=g(x) đồng biến trên (-1;2)
Chọn B
Cho hàm số y = f(x) có đạo hàm trên R và có đồ thị hàm số y=f'(x) như hình bên. Hàm số y=f(3-x) đồng biến trên khoảng nào dưới đây?
![]()
![]()
![]()
![]()
Câu 48: Cho hàm số y=f(x) có đạo hàm liên tục trên R và \(f'\left(x\right)=x\left(2x-1\right)\left(x^2+3\right)+2\). Hàm số \(y=f\left(3-x\right)+2x+2023\) đồng biến trên khoảng nào trong các khoảng sau?
A: \(\left(-\infty;3\right)\)
B: (3;5)
C: (2;5/2)
D: (5/2;3)
Câu 50: Cho hàm số y=f(x) có đạo hàm \(f'\left(x\right)=\left(x-1\right)^2\cdot\left(x^2-2x\right)\) với \(\forall x\in R\). Có bao nhiêu giá trị nguyên dương của tham số m để hàm số \(f\left(x^2-8x+m\right)\) có 5 điểm cực trị?
Cho hàm số y= f( x). Đồ thị hàm số y= f’(x) như hình bên dưới
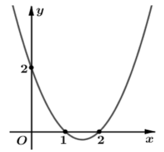
Hàm số g ( x ) = f ( x 2 + 2 x + 3 - x 2 + 2 x + 2 ) đồng biến trên khoảng nào sau đây?
A. ( - ∞ ; - 1 )
B. ( - ∞ ; - 1 / 2 )
C. ( 1 / 2 ; + ∞ )
D. ( - 1 ; + ∞ )
1. Cho hàm số y =f(x) có đạo hàm f'(x) = (x^2 -1)(x-2)^2(x-3) . Hàm số đồng biến ; nghịch biến trên khoảng nào? 2. Cho hàm số y = x^4 -2x^2 . Hàm số đồng biến ; nghịch biến trên khoảng nào?
1.
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)