Tìm tất cả các nghiệm của phương trình:
z 2 + 2 z + 5 = 0 .
A. 1+2i; 1-2i
B. 1+i; 1- i
C. -1+2i; -1-2i
D. -1+ i; -1- i
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho phương trình: ( z2 - z) ( z + 3) (z + 2) = 10 .Tính tổng tất cả các phần thực của các nghiệm phương trình trên.
A. -1
B. -2
C. -3
D. -4
Chọn D.
Phương trình đã cho tương đương với phương trình
z( z + 2) ( z - 1) ( z + 3)
Hay ( z2 + 2z) ( z2 + 2z - 3) = 10
Đặt t = z2 + 2z. Khi đó phương trình trở thành: t2 - 2t – 10 = 0.
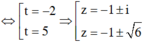
Vậy phương trình có các nghiệm: ![]()
Tổng tất cả các phần thực của các nghiệm phương trình đã cho là:
-1+ ( -1) + (-1) + ( -1) = -4.
Xác định tất cả các số thực m để phương trình
z 2 - 2 z + 1 - m = 0 có nghiệm phức z thỏa mãn z = 2 .
A. m = 1 ; m = 9 .
B. m = - 3
C. m = - 3 ; m = 1 ; m = 9 .
D. m = - 3 ; m = 9
Gọi S là tổng tất cả các số thực m để phương trình z 2 - 2 z + 1 - m = 0 có nghiệm thức z thỏa mãn z = 2 . Tính S
A. S = -3
B. S = 6
C. S = 10
D. S = 7
Tìm tất cả các nghiệm nguyên dương của phương trình \(\left(x+y\right)^2+y+3x=z^2+1\)
4) Tìm a thuộc Z để phương trình sau có nghiệm duy nhất là số nguyên
a^2x+2x=3(a+1-ax)
5) Tìm m để phương trình: (m^2+5)x=2-2mx
có nghiệm duy nhất đạt giá trị lớn nhất
6) Tìm tất cả các số thực a không âm sao cho phương trình: (a^2-4)x=a^2-ma+16 (ẩn x)
có nghiệm duy nhất là số nguyên
1. Tìm a,b ∈ Z+(a,b ≠1) để 2a+3b là số chính phương
2. Tìm nghiệm nguyên không âm của phương trình:
\(\left(2x+5y+1\right)\left(2020^{\left|x\right|}+y+x^2+x\right)=105\)
3. Tìm x,y,z ∈ Z+ t/m:
\(xy+y-x!=1;yz+z-y!=1;x^2-2y^2+2x-4y=2\)
4. Tìm tất cả các số nguyên tố p;q;r sao cho:
pq+qp=r
5. Tìm nghiệm nguyên tố của phương trình:
\(x^y+y^x+2022=z\)
6. CMR: Với n ∈ N và n>2 thì 2n-1 và 2n+1 không thể đồng thời là 2 số chính phương
Bài 2: Ta có:
\(\left(2x+5y+1\right)\left(2020^{\left|x\right|}+y+x^2+x\right)=105\) là số lẻ
\(\Rightarrow\left\{{}\begin{matrix}2x+5y+1\\2020^{\left|x\right|}+y+x^2+x\end{matrix}\right.\) đều lẻ
\(\Rightarrow y⋮2\)\(\Rightarrow2020^{\left|x\right|}⋮̸2\Leftrightarrow\left|x\right|=0\Leftrightarrow x=0\).
Thay vào tìm được y...
Lúc nãy bận thi online nên giờ mới làm tiếp được, bạn thông cảm.
Bài 4:
Do p; q; r là các SNT nên \(p^q+q^p>2^2+2^2=8\Rightarrow r>8\) nên r là SNT lẻ
Mà r lẻ thì trong 2 số \(p^q;q^p\) phải có 1 số lẻ, một số chẵn.
Do vai trò p; q như nhau nên không mất tính tổng quát ta giả sử p lẻ, q chẵn
\(\Rightarrow q=2\). Lúc này ta có:
\(p^2+2^p=r\)
+Xét p=3\(\Rightarrow p^2+2^p=r=17\left(tm\right)\) (Do p lẻ nên loại TH p=2)
+Xét p>3. Ta có:
\(\left\{{}\begin{matrix}p^2\equiv1\left(mod3\right)\\2^p\equiv\left(-1\right)^p\equiv-1\left(mod3\right)\end{matrix}\right.\)
\(\Rightarrow p^2+2^p\equiv1+\left(-1\right)\equiv0\left(mod3\right)\)
\(\Rightarrow\left(p^2+2^p\right)⋮3\) mà \(p^2+2^p>3\) nên là hợp số
\(\Rightarrow r\) là hợp số, không phải SNT, loại.
Vậy ta có \(\left(p;q;r\right)\in\left\{\left(3;2;17\right);\left(2;3;17\right)\right\}\) tm đề bài
Bài 6: Ta có 1SCP lẻ chia cho 4 dư 1.
Nếu 2n-1 là SCP thì ta có
\(2n-1\equiv1\left(mod4\right)\Leftrightarrow2n+1\equiv3\left(mod4\right)\)
Do đó 2n+1 không là SCP
\(\Rightarrowđpcm\)
Tìm tất cả các cặp số tự nhiên (n;z) thỏa mãn phương trình: \(2^n+12^2=z^2-3^2\)
Với \(0\le x;y;z\le1\). Tìm tất cả nghiệm của phương trình:
\(\frac{x}{1+y+xz}+\frac{y}{1+z+xy}+\frac{z}{1+x+yz}=\frac{3}{x+y+z}\)
Hãy tích nếu như bạn thông minh
Ai ko tích là bình thường
Còn ai dis là "..."
Ta có : \(\left(x-1\right)\left(y-1\right)\ge0\Rightarrow xy-\left(x+y\right)+1\ge0\)
\(\Rightarrow xy+z+1\ge x+y+z\Rightarrow\frac{y}{xy+z+1}\le\frac{y}{x+y+z}\)
Tương tự : \(\frac{x}{xz+y+1}\le\frac{x}{x+y+z}\); \(\frac{z}{yz+x+1}\le\frac{z}{x+y+z}\)
Cộng lại,ta được :
\(VT\le\frac{x}{x+y+z}+\frac{y}{x+y+z}+\frac{z}{x+y+z}=1\)( 1 )
Mà \(x+y+z\le3\Rightarrow VP=\frac{3}{x+y+z}\ge1\)( 2 )
Dấu "=" xảy ra khi x = y = z = 1
Từ ( 1 ) và ( 2 ) suy ra x = y = z = 1
Vậy ...
Nhờ các bạn giải giùm mình 5 bài luôn nhé! Mình đang cần gấp lắm! Mình cảm ơn.
1. Cho x,y,z khác 0 và (x+y+ z)^2 = x^2+y^2+z^2.
C/m 1/x^3 + 1/y^3 + 1/z^3= 3/x*y*z.
2. Giải phương trình:
x^3 + 3ax^2 + 3(a^2 -bc)x +a^3+b^3 +c^3
(Ẩn x)
3. Tìm nghiệm nguyên của phương trình:
(x+y)^3=(x-2)^3 + (y+2)^3 + 6
4. Tìm nghiệm nguyên dương thỏa mãn cả hai phương trình
x^3 + y^3 + 3xyz= z^3
z^3=(2x+2y)^3