Đáp án D

Ta có:  A E = B F = 1

Khi đó:  D E = A D 2 − A E 2 = 1

Khi quay hình chữ nhật DEFC quanh trục AB ta được hình trụ có thể tích là:

V 1 = π D E 2 . D C = π .1 2 .3 = 3 π

Khi quay tam giác AED quanh trục AB ta được hình nón có thể tích là:

V 2 = 1 3 π D E 2 . A E = 1 3 π .1 2 .1 = π 3

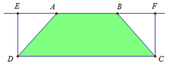
Do đó thể tích vận tròn xoay tạo thành khi cho hình thang quay quanh AB là:

V = V 1 − 2 V 2 = 7 π 3

Chọn đáp án D

Đáp án D

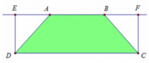
Ta có A E = B F = 1  Khi đó D E = A D 2 − A E 2 = 1  

Khi quay hình chữ nhật DEFC quay trục AB ta được hình trụ có thể tích là: V 1 = π . D E 2 . D C = π 1 2 .3 = 3 π

Khi quay tam giác AED quanh trục AB ta được hình nón

có thể tích là V 2 = 1 3 π . D E 2 . A E = 1 3 π .1 2 .1 = π 3 . Do đó thể tích vật tròn xoay tạo thành khi cho hình thang đó quay quanh AB là: V = V 1 − 2 V 2 = 7 π 3 .

Vì tứ giác ABCD là hình thang cân (gt).

=> AD = BC (Tính chất hình thang cân).

Mà BC = 2 (cm).

=> AD = 2 (cm).

Chu vi hình thang ABCD là:

AB + CD + BC + AD = 3 + 5 + 2 + 2 = 12 (cm).

p hình thang cân là :

3 + 5 + 2 + 2 = 12 cm

Đ/S : 12 cm

Giải giúp mình với 

BD=DC

=>góc DBC=góc DCB=72 độ

=>góc BDC=36 độ

=>góc ADB=36 độ

góc ADB=góc BDC

góc BDC=góc ABD

=>góc ABD=góc ADB

=>AD=AB(ĐPCM)

Kẻ đường cao BK và đường cao AH .

Xét tam giác ADC và tam giác BKC có :

\(AD=BC\left(gt\right)\)

\(\widehat{D}=\widehat{C}\)( vì ABCD là hình thang cân )

=> tam giác vuông ADC = tam giác vuông BKC ( cạnh huyền - góc nhọn )

\(\Rightarrow HD=KC=\frac{CD-HK}{2}=\frac{CD-AB}{2}=\frac{a-b}{2}\)

Xét tam giác AHD vuông tại H có :( Py-ta-go )

\(AD^2=AH^2+HD^2\)

\(=\left(\frac{a+b}{2}\right)^2+\left(\frac{a-b}{2}\right)^2\)

\(=\frac{2a^2+2b^2}{4}=\frac{a^2+b^2}{2}\)

Vậy \(AD=\sqrt{\frac{a^2+b^2}{2}}\)

Do AB//CD

=) \(\widehat{A}\)+\(\widehat{D}\)=180⁰ (2 góc vị trí trong cùng phía )

  100⁰ + \(\widehat{D}\)=180⁰

             ^{\(\widehat{D}\)}=180⁰ - 100⁰

           \(\widehat{D}\)= 80⁰

Xét tứ giác ABCD có :

\(\widehat{A}\)+\(\widehat{B}\)+\(\widehat{C}\)+\(\widehat{D}\)=360⁰

100⁰+120⁰+\(\widehat{C}\)+80⁰ =360⁰

 300⁰ +\(\widehat{C}\)=360⁰

         \(\widehat{C}\)= 60⁰

2) Từ B kẻ BE \(\perp\)CD

Xét tam giác ADH (\(\widehat{AH\text{D}}\)=90⁰) và BCE (\(\widehat{BEC}\)=90⁰) có:

           AD=BC (tính chất hình thang cân)

          \(\widehat{A\text{D}H}\)=\(\widehat{BCE}\)(tính chất hình thang cân)

=) Tam giác ADH = Tam giác BCE (cạch huyền - góc nhọn )

=)  DH= CE (2 cạch tương ứng )

Do AB//CD Mà AH\(\perp\)CD=) AH\(\perp\)AB

Xét tứ giác ABEH có

\(\widehat{BAH}\)= \(\widehat{AHE}\) = \(\widehat{BEH}\) = 90⁰

=) Tứ giác ABEH lá hình chữ nhật =) AB=HE=10 cm

Ta có : DH+HE+EC= 20 cm

         2DH+10=20

         2DH =10

           DH = 5 (cm)

xét tam giác vuông AHD 

Áp dụng định lí Pitago ta có

AD²=AH²+HD²

AD²=12²+5²

AD²= 144+25=169

AD=13 cm (đpcm)