Cho mặt phẳng (P): x + y - z + 3 = 0 và hai điểm A ( 2;1;2 ) , B ( 0;3;4 ) . Số các điểm thuộc mặt phẳng (P) sao cho tam giác ABM vuông tại M là.
A. 0
B. 1
C. 2
D. vô số điểm
Những câu hỏi liên quan
Phương trình mặt phẳng đi qua điểm A(1;1;1) và vuông góc với hai mặt phẳng
P
: x+y-z-20,
Q
: x-y+z-10
Đọc tiếp
Phương trình mặt phẳng đi qua điểm A(1;1;1) và vuông góc với hai mặt phẳng P : x+y-z-2=0, Q : x-y+z-1=0
Phương trình mặt phẳng đi qua điểm A(1;1;1) và vuông góc với hai mặt phẳng
(
P
)
:
x
+
y
-
z
-
2
0
,
(
Q
)
:
x
-
y
+
z
-
1
...
Đọc tiếp
Phương trình mặt phẳng đi qua điểm A(1;1;1) và vuông góc với hai mặt phẳng ( P ) : x + y - z - 2 = 0 , ( Q ) : x - y + z - 1 = 0 là
A. x + y + z - 3 = 0
B. x - 2y + z = 0
C. x + z - 2 = 0
D. x + y - 2 = 0
Viết phương trình mặt phẳng đi qua điểm A(1;1;1) và vuông góc với hai mặt phẳng x+y-z-2=0, x-y+z-1=0
A. x+y+z-3=0
B. y+z-2=0
C. x+z-2=0
D. x-2y+z=0
Mặt phẳng đi qua điểm A(1;1;1) và vuông góc với hai mặt phẳng x + y - z -2 0, x + y + z - 1 0 có phương trình là
Đọc tiếp
Mặt phẳng đi qua điểm A(1;1;1) và vuông
góc với hai mặt phẳng x + y - z -2 = 0,
x + y + z - 1 = 0 có phương trình là
Cho mặt phẳng
(
P
)
:
x
+
y
-
z
+
3
0
và hai điểm
A
(
2
;
1
;
2
)
,
B
(
0
;
3
;
4
)
. Số các điểm thuộc mặt phẳng (P) sao cho tam giác ABM vuông tại M là A. 0 B. 1 C. 2 D. vô số điểm
Đọc tiếp
Cho mặt phẳng ( P ) : x + y - z + 3 = 0 và hai điểm A ( 2 ; 1 ; 2 ) , B ( 0 ; 3 ; 4 ) . Số các điểm thuộc mặt phẳng (P) sao cho tam giác ABM vuông tại M là
A. 0
B. 1
C. 2
D. vô số điểm
Trong không gian Oxyz, viết phương trình mặt phẳng :
a) Qua điểm A (2;1;3) và vuông góc với đường thẳng Δ : x/1 = y/2 = z/3
b) Chứa hai điểm A (1;-1;2) , B (2;1;1) và vuông góc với mặt phẳng (P): x + y + z + 1 = 0
a. (P) vuông góc denta nên nhận (1;2;3) là 1 vtpt
Phương trình (P):
\(1\left(x-2\right)+2\left(y-1\right)+3\left(z-3\right)=0\)
\(\Leftrightarrow x+2y+3z-13=0\)
b. \(\overrightarrow{AB}=\left(1;2;-1\right)\) ; \(\overrightarrow{n_{\left(P\right)}}=\left(1;1;1\right)\)
\(\left[\overrightarrow{AB};\overrightarrow{n_{\left(P\right)}}\right]=\left(3;-2;-1\right)\)
Phương trình mp:
\(3\left(x-1\right)-2\left(y+1\right)-1\left(z-2\right)=0\)
\(\Leftrightarrow3x-2y-z-3=0\)
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng: (P): x + y + z - 2 0 (Q): x + 2y - z +3 0 và điểm A(1;0;4). Phương trình đường thẳng qua A và cùng song song với (P) và (Q).
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz,
cho hai mặt phẳng:
(P): x + y + z - 2 = 0
(Q): x + 2y - z +3 = 0
và điểm A(1;0;4). Phương trình đường thẳng qua A và cùng song song với (P)
và (Q).
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P): x+y+z-20, (Q): x+2y-z+30 và điểm A(1;0;4). Phương trình đường thẳng qua A và cùng song song với (P) và (Q) là: A.
d
:
x
-
1
-
3
y
2
...
Đọc tiếp
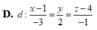
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P): x+y+z-2=0, (Q): x+2y-z+3=0 và điểm A(1;0;4). Phương trình đường thẳng qua A và cùng song song với (P) và (Q) là:
A. d : x - 1 - 3 = y 2 = z - 4 1
B. d : x - 1 3 = y 1 = z - 4 1
C. d : x - 1 - 3 = y - 1 = z - 4 1
D. d : x - 1 - 3 = y 2 = z - 4 - 1
Trong không gian Oxyz, viết phương trình đường thẳng :
a) Qua điểm A (1;2-1) và vuông góc với mặt phẳng (P) : 3x - 2y + 2z + 1 = 0
b) Qua điểm A(1;-2;3) và song song với hai mặt phẳng (P) : x + y + z + 1 = 0, (P') : x - y + z - 2 = 0
c) Qua điểm M(-1;1;3) và vuông góc với hai đường thẳng Δ : x-1/3 = y+3/2 = z-1/1 , Δ' : x+1/1 = y/3 = z/-2
a. Mặt phẳng (P) có (3;-2;2) là 1 vtpt nên d nhận (3;-2;2) là 1 vtcp
Phương trình tham số d: \(\left\{{}\begin{matrix}x=1+3t\\y=2-2t\\z=-1+2t\end{matrix}\right.\)
b. \(\overrightarrow{n_{\left(P\right)}}=\left(1;1;1\right)\) ; \(\overrightarrow{n_{\left(P'\right)}}=\left(1;-1;1\right)\)
\(\left[\overrightarrow{n_{\left(P\right)}};\overrightarrow{n_{\left(P'\right)}}\right]=\left(2;0;-2\right)=2\left(1;0;-1\right)\)
\(\Rightarrow\) d nhận (1;0;-1) là 1 vtcp nên pt có dạng: \(\left\{{}\begin{matrix}x=1+t\\y=-2\\z=3-t\end{matrix}\right.\)
c. \(\overrightarrow{u_{\Delta}}=\left(3;2;1\right)\) ; \(\overrightarrow{u_{\Delta'}}=\left(1;3;-2\right)\)
\(\left[\overrightarrow{u_{\Delta}};\overrightarrow{u_{\Delta'}}\right]=\left(-7;7;7\right)=7\left(-1;1;1\right)\)
Đường thẳng d nhận (-1;1;1) là 1 vtcp nên pt có dạng: \(\left\{{}\begin{matrix}x=-1-t\\y=1+t\\z=3+t\end{matrix}\right.\)
Đúng 0
Bình luận (0)