Giả sử đường tròn cố định (C) tâm I bán kính r nằm trên mặt phẳng (P). Xét đường thẳng d qua I và vuông góc với mặt phẳng (P). Đường thẳng d được gọi là trục của đường tròn. Giả sử O là tâm của mặt cấu (S) chứa đường tròn (C) thì O cách đều mọi điểm của (C).Vì vậy chân đường vuông góc hạc từ O xuống mặt phẳng (P) chính là tâm I của (C). Điều đó xảy ra khi và chỉ khi điểm O εd

Kết luận: Tập hợp tâm các mặt cấu luôn luôn chứa một đường tròn cố định cho trước là đường thẳng d vuông góc với mặt phẳng chứa đường tròn tại tâm của nó.

Tập hợp tâm các mặt cầu luôn luôn đi qua hai điểm cố định A và B cho trước là đường trung trực của đoạn thẳng AB

Đáp án B

Tập hợp tâm các mặt cầu luôn đi qua hai điểm cố định A và B cho trước là một mặt phẳng trung trực của AB

Đáp án B

Tập hợp tâm các mặt cầu luôn đi qua hai điểm cố định A và B cho trước là một mặt phẳng trung trực của AB

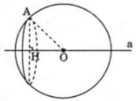
Gọi (P) là mặt phẳng đi qua A và vuông góc với đường thẳng a tại H. Khi đó (P) và H cố định.

Ta có: (P) cắt mặt cầu S(O; R) theo đường tròn tâm H và bán kính HA không đổi.

Vậy các mặt cầu tâm O bán kính R = OA luôn đi qua đường tròn cố định tâm H bán kính bằng HA.

Xét mặt phẳng (P) qua điểm A và (P) vuông góc với đường thẳng a. GỌi giao của (P) với a là điểm I. Xét mặt cầu tâm O bán kính r = OA; mặt cầu này giao với mặt phẳng (P) theo đường tròn tâm I là hình chiếu vuông góc của O lên (P) và bán kính IA = r² cố định

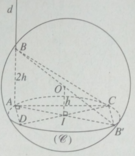
Ta có AH ⊥ DC. Do đó khi CD di động, điểm H luôn luôn nhìn đọan thẳng AI dưới một góc vuông. Vậy tập hợp các điểm H là đường tròn đường kính AI nằm trong mặt phẳng ( α ).

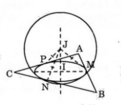
* Xét mặt cầu (S) tâm J, bán kính R và tiếp xúc với ba cạnh: AB, BC, AC lần lượt tại M, N và P.

Gọi I là hình chiếu vuông góc của J lên mp (ABC) ⇒ IJ ⊥ (ABC)

* Ta có: 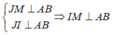 (định lí 3 đường vuông góc)

Chứng minh tương tự có: 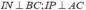 (1)

* Xét ba tam giác JIM; JIN và JIP có:

⇒ ∆ JIM = ∆ JIN = ∆JIP (ch- cgv)

⇒ IN = IM = IP (2)

Từ (1) và (2) suy ra, I là tâm đường tròn nội tiếp tam giác ABC.

* Lấy điểm J thuộc trục đường tròn nội tiếp tam giác ABC.

Đường tròn nội tiếp tam giác ABC tiếp xúc với ba cạnh AB, BC và CA lần lượt taị M, N và P.

Ta có: 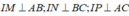 (1)

Mặt khác; IM = IN = IP = r.

⇒ ∆ JIM = ∆ JIN = ∆JIP (c-g-c)

⇒ JM = JN = JP (2)

Từ (1) và (2) suy ra, mặt cầu (S) tâm J tiếp xúc với ba cạnh của tam giác ABC.

Vậy tập hợp tâm các mặt cầu tiếp xúc với ba cạnh của tam giác ABC cho trước là trục đường tròn nội tiếp tam giác ABC,

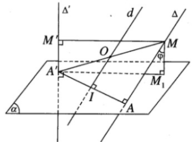
Gọi I là trung điểm của đoạn AA’. Ta có IO // Δ nên tâm O di động trên đường thẳng d cố định đi qua I và song song với ∆ . Mặt cầu tâm O đi qua hai điểm cố định A, A’ , có tâm di động trên đường trung trực d cố định của đoạn AA’. Vậy mặt cầu tâm O luôn luôn chứa đường tròn cố định tâm I có đường kính AA’ nằm trong mặt phẳng AA’ và vuông góc với d.