Đáp án B
Tập hợp tâm các mặt cầu luôn đi qua hai điểm cố định A và B cho trước là một mặt phẳng trung trực của AB
Đáp án B
Tập hợp tâm các mặt cầu luôn đi qua hai điểm cố định A và B cho trước là một mặt phẳng trung trực của AB
Cho mặt trụ (T) và một điểm S cố định nằm ngoài (T). Một đường thẳng Δ luôn đi qua S và cắt (T) tại hai điểm A, B (A, B có thể trùng nhau). Gọi M là trung điểm của đoạn thẳng AB. Tập hợp các điểm M là
A. Một mặt phẳng đi qua S.
B. Một mặt cầu đi qua S.
C. Một mặt nón có đỉnh là S.
D. Một mặt trụ.
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d : x - 2 1 = y - 5 2 = z - 2 1 , d ' : x - 2 1 = y - 1 - 2 = z - 2 1 và hai điểm A(a;0;0), A’(0;0;b). Gọi (P) là mặt phẳng chứa d và d’; H là giao điểm của đường thẳng AA’ và mặt phẳng (P). Một đường thẳng thay đổi trên (P) nhưng luôn đi qua H đồng thời D cắt d và d’ lần lượt tại B, B’. Hai đường thẳng AB, A’B’ cắt nhau tại điểm M. Biết điểm M luôn thuộc một đường thẳng cố định có vectơ chỉ phương u → = 15 ; - 10 ; - 1 (tham khảo hình vẽ). Tính a+b
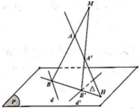
A. 8
B. 9
C. -9
D. 6
Với điểm O cố định thuộc mặt phẳng (P) cho trước, xét đường thẳng l thay đổi đi qua O và tạo với (P) một góc 300. Tập hợp các đường thẳng l trong không gian là
A. một mặt trụ
B. hai đường thẳng
C. một mặt trụ
D. một mặt nón
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
d : x - 2 1 = y - 5 2 = z - 2 1 , d ' : x - 2 1 = y - 1 - 2 = z - 2 1 và hai điểm A a ; 0 ; 0 , A ' 0 ; 0 ; b . Gọi (P) là mặt phẳng chứa d và d '; H là giao điểm của đường thẳng AA' và mặt phẳng (P). Một đường thẳng ∆ thay đổi trên (P) nhưng luôn đi qua H đồng thời ∆ cắt d và d ' lần lượt là B, B '. Hai đường thẳng AB, A'B' cắt nhau tại điểm M. Biết điểm M luôn thuộc một đường thẳng cố định có vectơ chỉ phương u → = 15 ; - 10 ; - 1 (tham khảo hình vẽ). Tính T= a+b
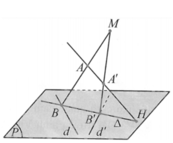
A. T = 8
B. T = 9
C. T = - 9
D. T = 6
Trong không gian, cho hai điểm A, B cố định và độ dài đoạn thẳng AB bằng 4. Biết rằng tập hợp các điểm sao cho M A = 3 M B là một mặt cầu. Bán kính của mặt cầu bằng
A. 3
B. 3 2
C. 9 2
D. 1
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d : x − 2 1 = y − 5 2 = z − 2 1 , d ' : x − 2 1 = y − 1 − 2 = z − 2 1 và hai điểm A a ; 0 ; 0 , A ' 0 ; 0 ; b . Gọi (P) là mặt phẳng chứa d và d¢; H là giao điểm của đường thẳng AA¢ và mặt phẳng (P). Một đường thẳng D thay đổi trên (P) nhưng luôn đi qua H đồng thời D cắt d và d¢ lần lượt tại B, B¢. Hai đường thẳng A B , A ' B ' cắt nhau tại điểm M. Biết điểm M luôn thuộc một đường thẳng cố định có véc tơ chỉ phương u → 15 ; − 10 ; − 1 (tham khảo hình vẽ). Tính T = a + b

A. T = 8
B. T = 9
C. T = - 9
D. T = 6
Trong không gian Oxyz, cho mặt cầu S : x − 1 2 + y − 2 2 + z − 3 2 = 25 v à M 4 ; 6 ; 3 . . Qua M kẻ các tia Mx, My, Mz đôi một vuông góc với nhau và cắt mặt cầu tại các điểm thứ hai tương ứng là A, B, C. Biết mặt phẳng (ABC) luôn đi qua một điểm cố định H a ; b ; c . Tính a + 3 b − c
A. 9
B. 20
C. 14
D. 11
Cho mặt cầu (S) tâm O, bán kính bằng 2 và mặt phẳng (P). Khoảng cách từ O đến (P) bằng 4. Từ điểm M thay đổi trên (P) kẻ các tiếp tuyến MA;MB;MC tới (S) với A;B;C là các tiếp điểm. Biết mặt phẳng (ABC) luôn đi qua một điểm I cố định. Tính độ dài đoạn OI.
A. 3
B. 3 2
C. 1/2
D. 1
Trong không gian cho hai điểm A, B cố định và độ dài đoạn thẳng AB bằng 4. Biết rằng tập hợp các điểm M sao cho MA = 3MB là một mặt cầu. Bán kính của mặt cầu bằng:
A. 3
B. 9 2
C. 1
D. 3 2