Đáp án B
Tập hợp tâm các mặt cầu luôn đi qua hai điểm cố định A và B cho trước là một mặt phẳng trung trực của AB
Đáp án B
Tập hợp tâm các mặt cầu luôn đi qua hai điểm cố định A và B cho trước là một mặt phẳng trung trực của AB
Cho mặt cầu tâm O bán kính r. Gọi ( α ) là mặt phẳng cách tâm O một khoảng h (0 < h < r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng ( α ) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C). Tìm tập hợp các điểm H, hình chiếu của B trên CD khi CD chuyển động trên đường tròn (C).
Cho mặt trụ (T) và một điểm S cố định nằm ngoài (T). Một đường thẳng ∆ luôn đi qua S và cắt (T) tại hai điểm A, B (A, B có thể trùng nhau). Gọi M là trung điểm của đoạn thẳng AB. Tập hợp các điểm M là
A. Một mặt phẳng đi qua S.
B. Một mặt cầu đi qua S.
C. Một mặt nón có đỉnh là S.
D. Một mặt trụ.
Cho một điểm A cố định và một đường thẳng a cố định không đi qua A. Gọi O là một điểm thay đổi trên a. Chứng minh rằng các mặt cầu tâm O bán kính r = OA luôn luôn đi qua một đường tròn cố định
Trong mặt phẳng ( α ) cho hình vuông ABCD có cạnh bằng a. Trên đường thẳng Ax vuông góc với ( α ) ta lấy một điểm S tùy ý, dựng mặt phẳng ( β ) đi qua A và vuông góc với đường thẳng SC. Mặt phẳng ( β ) cắt SB, SC, SD lần lượt tại B’ , C’, D’. Chứng minh rằng các điểm A, B, C, D, B’, C’ , D’ luôn luôn thuộc một mặt cầu cố định.
Cho mặt cầu tâm O bán kính r. Gọi ( α ) là mặt phẳng cách tâm O một khoảng h (0 < h < r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng ( α ) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C). Chứng minh các tổng AD 2 + BC 2 và AC 2 + BD 2 có giá trị không đổi
Cho hai điểm A, B phân biệt. Tập hợp tâm những mặt cầu đi qua A và B là
A. Mặt phẳng trung trực của đoạn thẳng AB
B. Đường trung trực của AB
C. Mặt phẳng song song với đường thẳng AB
D. Trung điểm của đoạn AB
Tìm tập hợp tâm các mặt cầu luôn luôn đi qua hai điểm cố định A và B cho trước.
Trong không gian Oxyz, cho mặt cầu S : x 2 + y 2 + x + 2 2 = 16 và điểm A(m;m;2) nằm ngoài mặt cầu. Từ A kẻ các tiếp tuyến đến mặt cầu (S), gọi P m là mặt phẳng chứa các tiếp điểm, biết P m luôn đi qua một đường thẳng d cố định, phương trình đường thẳng d là:
A. 
B. 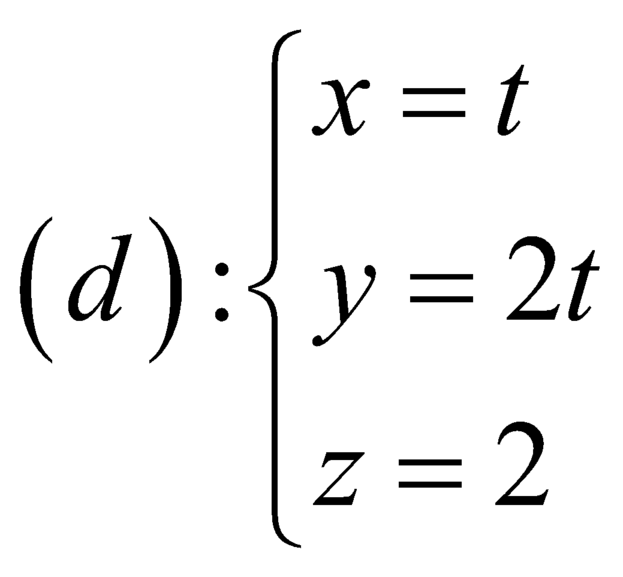
C. 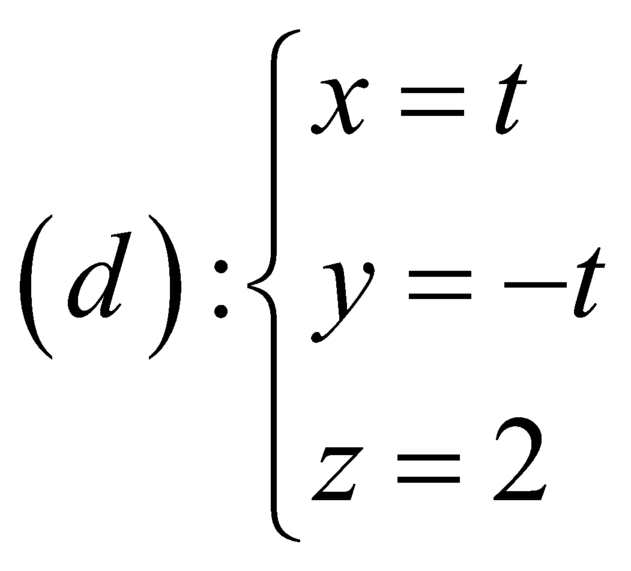
D. 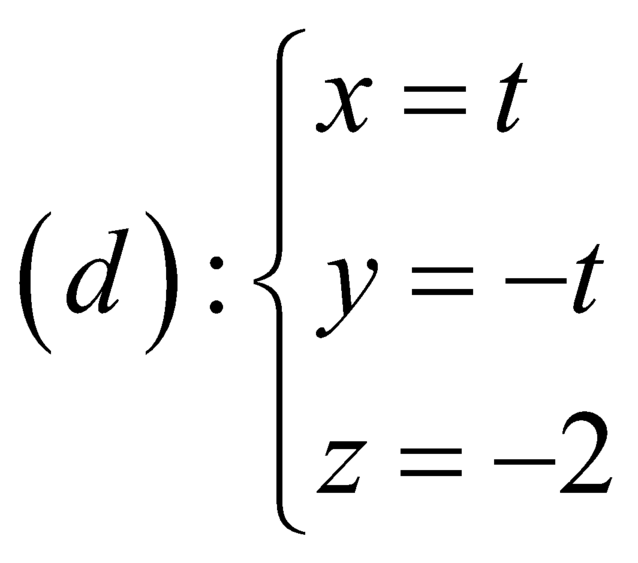 .
.
Cho mặt cầu tâm O bán kính r. Gọi ( α ) là mặt phẳng cách tâm O một khoảng h (0 < h < r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng ( α ) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C). Với vị trí nào của CD thì diện tích tam giác BCD lớn nhất?