Gọi (C) là đồ thị hàm số y = x + 2 2 x - 1 . Trong các mệnh đề sau, mệnh đề nào sai?
A. (C) có tiệm cận ngang là y = 1 2
B. (C) có đúng một trục đối xứng.
C. (C) có tiệm cận đứng là x = 1 2
D. (C) có đúng một tâm đối xứng.
giúp mk câu này vs ạ
Cho hàm số y = x có đồ thị là đường thẳng (d1).
hàm số y = - x + 3 có đồ thị là đường thẳng (d2).
và hàm số y = m x + 2 có đồ thị là đường thẳng (d3).
a) Vẽ (d1) và (d2) trên cùng mặt phẳng tọa độ Oxy.
b) Gọi giao điểm của (d1) và (d2) là A, giao điểm của (d2) và trục Ox là B. Tính diện tích tam giác AOB .
c) Xác định điểm D thuộc đường thẳng (d1) và E thuộc (d2) sao cho hoành độ của chúng đều bằng 3.
d) Tìm m để (d3) song song với (d1).
e) Tìm m để ba đường thẳng đồng qui.
f) Chứng minh rằng (d3) luôn đi qua một điểm cố định với mọi m.
g) Tìm m để khoảng cách từ gốc tọa độ O đến đường thẳng (d3) bằng 1
h) Tìm m để đường thẳng (d3) cắt (d2) tại điểm nằm ở góc phần tư thứ III.
d: Để hai đường thẳng song song thì m=1
Bài 1 a) Khảo sát và vẽ đồ thị hàm số y=x³-2x²+x (C) b) từ đồ thị (C) suy ra đồ thị các hàm số sau: y=|x³-2x²+x|, y=|x|³ -2x²+|x| Bài 2: Khảo sát và vẽ đồ thị hàm số y=x⁴-2x²-3 (C). Từ đồ thị (C) suy ra đồ thị hàm số y=|y=x⁴-2x²-3|
Cho hai hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e với a ≠ 0 và g(x)= p x 2 + q x - 3 c ó đồ thị như hình vẽ bên dưới. Đồ thị hàm số y=f(x) đi qua gốc tọa độ và cắt đồ thị hàm số y=g(x) tại bốn điểm có hoành độ lần lượt là -2;-1;1 và m. Tiếp tuyến của đồ thị hàm số y=f(x)-g(x) tại điểm có hoành độ x=-2 có hệ số góc bằng -15/2. Gọi (H) là hình phẳng giới hạn bởi đồ thị hai hàm số y=f(x) và y=g(x) (phần được tô đậm trong hình vẽ). Diện tích của hình (H) bằng

A. 1553 120
B. 1553 240
C. 1553 60
D. 1553 30
Cho hàm số 3 2 y x x = − +3 có đồ thị (C) . Gọi 1 d , 2 d là tiếp tuyến của đồ thị (C) vuông góc với đường thẳng x y − + = 9 1 0 . Tính khoảng cách giữa hai đường thẳng 1 d , 2 d .
Cho hàm số \(y=x^4-2mx^2+m\) có đồ thị (C) với m là tham số thực. Gọi A là điểm thuộc đồ thị (C) có hoành độ bằng 1. Tìm m để tiếp tuyến \(\Delta\) với đồ thị (C) tại A cắt đượng tròn \(\left(\lambda\right):x^2+\left(y-1\right)^2=4\) tạo thành 1 dây cung có độ dài nhỏ nhất
x^2+(y-1)^2=4
=>R=2 và I(0;1)
A(1;1-m) thuộc (C)
y'=4x^3-4mx
=>y'(1)=4-4m
PT Δsẽ là y=(4-m)(x-1)+1-m
Δ luôn đi qua F(3/4;0) và điểm F nằm trong (λ)
Giả sử (Δ) cắt (λ) tại M,N
\(MN=2\sqrt{R^2-d^2\left(I;\Delta\right)}=2\sqrt{4-d^2\left(I;\Delta\right)}\)
MN min khi d(I;(Δ)) max
=>d(I;(Δ))=IF
=>Δ vuông góc IF
Khi đó, Δ có 1 vecto chỉ phương là: vecto u vuông góc với vecto IF=(3/4;p-1)
=>vecto u=(1;4-4m)
=>1*3/4-(4-4m)=0
=>m=13/16
Biết đồ thị (C) ở hình bên là đồ thị hàm số y = a x a > 0 , a ≠ 1 . Gọi (C’) là đường đối xứng với (C) qua đường thẳng y=x
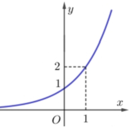
Hỏi (C’) là đồ thị của hàm số nào dưới đây?
A. y = log 1 2 x .
B. y = 2 x .
C. y = 1 2 x .
D. y = log 2 x .
Cho hàm số y = x\(^2\) có đồ thị (P\(_1\)) và hàm số y = -x\(^2\) có đồ thị (P\(_2\))
a) Vẽ đồ thị của các hàm số này trên cùng một mặt phẳng tọa độ.
b) Gọi A là một điểm bất kì trên (P\(_1\)) và B là điểm đối xứng với A qua trục hoành. Chứng minh rằng điểm B nằm trên (P\(_2\)).
Cho hàm số y= 2+ x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = 2 - x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x - 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x + 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Gọi (C) là đồ thị của hàm số y = lo 2018 x và C ' là đồ thị của hàm số y = f(x) , C ' đối xứng với (C) qua trục tung. Hàm số y = f x đồng biến trên khoảng nào sau đây?
![]()
![]()
![]()
![]()