Cho n > 1 là một số nguyên dương. Giá trị của 1 log 2 n ! + 1 log 3 n ! + 1 log 4 n ! + . . . + 1 log n n ! bằng
A.
B. 1
C. 0
D. n!
Những câu hỏi liên quan
7 tháng 5 2022 lúc 21:27
Cho số thực dương x,left(xne1,xnedfrac{1}{2}right) thỏa mãn log_xleft(16xright)log_{2x}left(8xright). Giá trị log_xleft(16xright) bằng logdfrac{m}{n} với m và n là các số nguyên dương và phân số dfrac{m}{n} tối giản. Tổng m+n bằng?Giải thích cho mình dòng bôi vàng ở dưới, mình cảm ơn nhiều ♥
Đọc tiếp
Cho số thực dương \(x,\left(x\ne1,x\ne\dfrac{1}{2}\right)\) thỏa mãn \(log_x\left(16x\right)=log_{2x}\left(8x\right)\). Giá trị \(log_x\left(16x\right)\) bằng \(log\dfrac{m}{n}\) với \(m\) và \(n\) là các số nguyên dương và phân số \(\dfrac{m}{n}\) tối giản. Tổng \(m+n\) bằng?
Giải thích cho mình dòng bôi vàng ở dưới, mình cảm ơn nhiều ♥
Cho hàm số
y
ln
2
x
-
a
-
2
m
ln
2
x
-
a
+
2
(m là tham số thực), trong đó x,...
Đọc tiếp
Cho hàm số y = ln 2 x - a - 2 m ln 2 x - a + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0 (với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thỏa mãn M a x 1 ; e 2 y = 1 . Số phần tử của S là:/
A. 0
B. 1
C. 2
D. Vô số
Chọn B
Cách giải: Ta có:
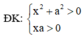
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0
Đúng 0
Bình luận (0)
Cho hàm số
y
ln
2
x
-
a
-
2
m
ln
2
x
-
a
+
2
(m là tham số thực), trong đó x,...
Đọc tiếp
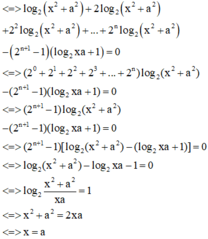
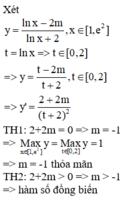
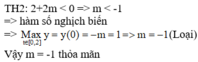
Cho hàm số y = ln 2 x - a - 2 m ln 2 x - a + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 x 2 + a 2 - 2 n - 1 - 1 log 2 x a + 1 = 0 (với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thỏa mãn M a x 1 , e 2 y = 1 . Số phần tử của S là:
A. 0
B. 1
C. 2
D. Vô số
Cho hàm số
y
ln
(
2
x
-
a
)
-
2
m
ln
(
2
x
-
a
)
+...
Đọc tiếp
Cho hàm số y = ln ( 2 x - a ) - 2 m ln ( 2 x - a ) + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + . . . + log . . . 2 ( x 2 + a 2 ) - ( 2 n + 1 - 1 ) ( log 2 x a + 1 ) = 0
(với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thoả mãn m a x [ 1 ; e 2 ] y = 1 . Số phần tử của S là
A. 0
B. 1
C. 2
D. Vô số
Cho x ϵ (0;π/2). Biết log(sinx)+log(cosx)-1 và log(sinx+cosx)1/2(logn-1). Giá trị của n là A. 11. B. 12. C. 10. D. 15.
Đọc tiếp
Cho x ϵ (0;π/2). Biết log(sinx)+log(cosx)=-1 và log(sinx+cosx)=1/2(logn-1). Giá trị của n là
A. 11.
B. 12.
C. 10.
D. 15.
BÀI 2. ĐỘ CAO CỦA DÃY SỐ DOCAO13.PASTa gọi độ cao của một số nguyên dương K là tổng giá trị các chữ số của K.Ví dụ: số 25362 có độ cao là 18. Cho dãy số nguyên dương A gồm N phần tử a 1 ,a 2 , ..., a N .(1 ≤ N ≤ 1000, 1 ≤ i ≤ N, 0 < a i ≤ 2147483647)Yêu cầu: Hãy tính độ cao của các phần tử trong dãy số A.Dữ liệu vào: Ghi trong file văn bản DOCAO13.INP có cấu trúc như sau:- Dòng 1: Ghi số nguyên dương N, là số lượng phần tử của dãy số.- Dòng 2: Ghi N số nguyên dương, số thứ i là giá trị của ph...
Đọc tiếp
BÀI 2. ĐỘ CAO CỦA DÃY SỐ DOCAO13.PAS
Ta gọi độ cao của một số nguyên dương K là tổng giá trị các chữ số của K.
Ví dụ: số 25362 có độ cao là 18. Cho dãy số nguyên dương A gồm N phần tử a 1 ,
a 2 , ..., a N .(1 ≤ N ≤ 1000, 1 ≤ i ≤ N, 0 < a i ≤ 2147483647)
Yêu cầu: Hãy tính độ cao của các phần tử trong dãy số A.
Dữ liệu vào: Ghi trong file văn bản DOCAO13.INP có cấu trúc như sau:
- Dòng 1: Ghi số nguyên dương N, là số lượng phần tử của dãy số.
- Dòng 2: Ghi N số nguyên dương, số thứ i là giá trị của phần tử a i trong dãy số,
các số được ghi cách nhau ít nhất một dấu cách.
Dữ liệu ra: Ghi ra file văn bản DOCAO13.OUT theo cấu trúc như sau:
- Dòng 1: Ghi N số nguyên dương t 1 , t 2 , ..., t N, t i là độ cao của số của a i . Các số
được ghi cách nhau một dấu cách.
Ví dụ:
DOCAO13.INP DOCAO13.OUT
5 13 5 5 10 9
const fi='docao13.inp'
fo='docao13.out'
var f1,f2:text;
a:array[1..100]of integer;
i,n:integer;
//chuongtrinhcon
function kq(x:integer):integer;
var t,k:integer;
begin
t:=0;
while (x>0) do
begin
k:=x mod 10;
t:=t+k;
x:=x div 10;
end;
kq:=t;
end;
//chuongtrinhchinh
begin
assign(f1,fi); reset(f1);
assign(f2,fo); rewrite(f2);
readln(f1,n);
for i:=1 to n do
read(f1,a[i]);
for i:=1 to n do
write(f2,kq(a[i]):4);
close(f1);
close(f2);
end.
Đúng 1
Bình luận (0)
Cho n 1 là một số nguyên dương. Giá trị của
1
log
2
n
!
+
1
log
3
n
!
+
1
log
4
n
!
+
.
.....
Đọc tiếp
Cho n >1 là một số nguyên dương. Giá trị của 1 log 2 n ! + 1 log 3 n ! + 1 log 4 n ! + . .. + 1 log n n ! bằng
A. 1
B. 1 2
C. n !
D. 0
Cho n 1 là một số nguyên dương. Giá trị của
1
log
2
n
!
+
1
log
3
n
!
+
1...
Đọc tiếp
Cho n > 1 là một số nguyên dương. Giá trị của 1 log 2 n ! + 1 log 3 n ! + 1 log 4 n ! + . . . + 1 log n n ! bằng
A. 1/2
B. 1
C. 0
D. n!
Có bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình dưới đây:
log (x - 40) + log (60 - x) < 2?
A. 20
B. 10
C. Vô số
D. 18
Đáp án D
Điều kiện 40 < x < 60
Vậy x cần tìm theo yêu cầu đề là các số nguyên dương chạy từ 41 đến 59; trừ giá trị 50. Có tất cả 18 giá trị thỏa mãn.
Đúng 0
Bình luận (0)