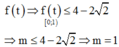Đáp án B.

Phương pháp: 

Bất phương trình m ≥ f x ,    x ∈ D có nghiệm khi và chỉ khi m ≥ M i n D f x .  

Cách giải:

ĐKXĐ:  0 < x < 1

3 log x ≤ 2 log m x − x 2 − 1 − x 1 − x ⇔ m x − x 2 − 1 − x 1 − x ≥ x x

⇔ m ≥ x x + 1 − x 1 − x x − x 2 ,    x ∈ 0 ; 1

Để bất phương trình đã cho có nghiệm thực thì m ≥ M i n 0 ; 1 f x , f x = x x + 1 − x 1 − x x − x 2  

Xét

f x = x x + 1 − x 1 − x x − x 2 = x + 1 − x 1 − x x − 1 x x − 1 , x ∈ 0 ; 1  

Đặt t = x + 1 − x ,    t ∈ 1 ; 2  

Khi đó,  

f x = x + 1 − x 1 − x 1 − x x 1 − x = t 1 − t 2 − 1 2 t 2 − 1 2 = t 3 − t 2 t 2 − 1 = 3 t − t 3 t 2 − 1 = g t

g ' t = − t 4 − 3 t 2 − 1 2 < 0 ,     ∀ t ∈ 1 ; 2  

⇒ g t min = g 2 = 3 2 − 2 2 2 − 1 = 2 ⇒ M i n 0 ; 1 f x = 2 ⇒ m ≥ 2  

Mà

m ∈ − 9 ; 9 ⇒ m ∈ 2 ; 3 ; 4 ; ... ; 8 ⇒

Có 7 giá trị thỏa mãn.

Đáp án C

ĐKXĐ: \(x\ge0\)

- Với \(x=0\) ko phải là nghiệm

- Với \(x>0\) chia 2 vế cho \(x\) ta được:

\(\dfrac{x^2+4}{x}+2-m=4\sqrt{\dfrac{x^2+4}{x}}\)

Đặt \(\sqrt{\dfrac{x^2+4}{x}}=t\ge2\)

\(\Rightarrow t^2-4t+2=m\)

Xét hàm \(f\left(t\right)=t^2-4t+2\) với \(t\ge2\)

\(\Rightarrow f\left(t\right)\ge f\left(2\right)=-2\Rightarrow m\ge-2\)

Có \(2018-\left(-2\right)+1=2021\) giá trị nguyên của m

ĐK: \(-2\le x\le2\)

Đặt \(\sqrt{x+2}+\sqrt{2-x}=t\left(2\le t\le2\sqrt{2}\right)\)

Phương trình đã cho trở thành:

\(t+t^2-4+2m+3=0\)

\(\Leftrightarrow2m=f\left(t\right)=-t^2-t+1\)

Phương trình đã cho có nghiệm khi \(minf\left(t\right)\le2m\le maxf\left(t\right)\)

\(\Leftrightarrow-7-2\sqrt{2}\le2m\le-5\)

\(\Leftrightarrow\dfrac{-7-2\sqrt{2}}{2}\le m\le-\dfrac{5}{2}\)

Chọn đáp án A

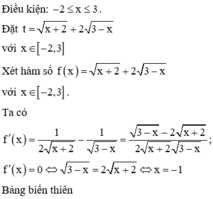
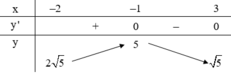
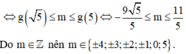
Vậy số giá trị nguyên của m để phương trình có nghiệm là 10.

để pt có hai nghiệm trái dấu: 

 \(1.\left(m-10\right)< 0\\ =>m< 10\\ =>m=\left\{1;2;3;4;5;6;7;8;9\right\}\\ =>C\)

Đáp án B

PT

Đặt 

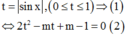
Để (1) có nghiệm thì (2) có nghiệm  có nghiệm

Suy ra 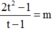có nghiệm 

Xét hàm số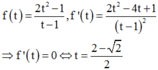 

Lập bảng biến thiên hàm số