Biết rằng parabol y = 1 24 x 2 chia hình phẳng giới hạn bởi elip có phương trình x 2 16 + y 2 1 = 1 thành hai phần có diện tích lần lượt là S1,S2với S1<S2. Tỉ số của S 1 S 2 bằng
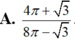
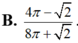
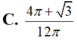

Biết rằng parabol y = 1 24 x 2 chia hình phẳng giới hạn bởi elip có phương trình x 2 16 + y 2 1 = 1 thành hai phần có diện tích lần lượt S 1 , S 2 là với S 1 < S 2 . Tỉ số của S 1 S 2 bằng
A . 4 π + 3 8 π - 3
B . 4 π - 2 8 π + 2
C . 4 π + 3 12 π
D . 8 π - 3 12 π
Biết rằng parabol
y
=
1
24
x
2
chia hình phẳng giới hạn bởi elip có phương trình
x
2
16
+
y
2
1
=
1
thành hai
phần có diện tích lần lượt là
S
1
,
S
2
với
S
1
<
S
2
. Tỉ số
S
1
S
2
bằng
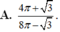
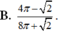
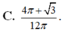
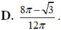
Đáp án A
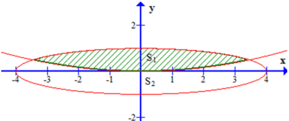
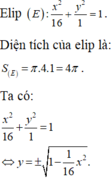
Nhận thấy S 1 là diện tích hình phẳng giới hạn bởi parabol y = 1 24 x 2 và phần elip nằm phía trên trục hoành.
Ta có phương trình hoành độ giao điểm của parabol y = 1 24 x 2 và elip x 2 16 + y 2 1 = 1 là
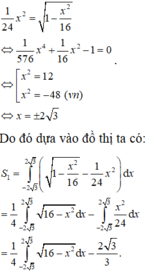
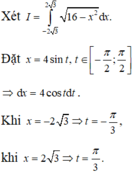
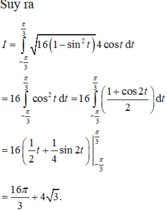
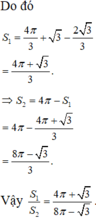
Cho (H) là hình phẳng giới hạn bởi parabol y = 3 2 x 2 và nửa đường elip có phương trình y = 1 2 4 - x 2 (với - 2 ≤ x ≤ 2 ) (phần tô đậm trong hình vẽ). Diện tích của (H) bằng:
A. 2 π + 3 6
B. 2 π + 3 12
C. 2 π - 3 6
D. 4 π + 3 6
Chọn đáp án A
Phương trình hoành độ giao điểm của parabol y = 3 2 x 2 và nửa đường elip
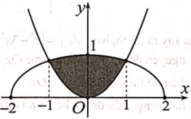
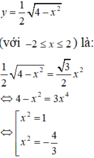
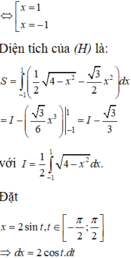
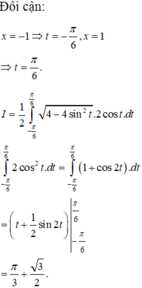
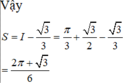
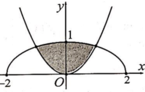
Cho (H) là hình phẳng giới hạn bởi parabol y = 3 2 x 2 và nửa đường elip có phương trình y = 1 2 4 - x 2 ( v ớ i - 2 ≤ x ≤ 2 ) (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
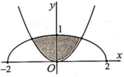
A. 2 π + 3 6
B. 2 π + 3 12
C. 2 π - 3 6
D. 4 π + 3 6
Cho hình phẳng (H) giới hạn bởi Parabol y = x 2 12 và đường cong có phương trình y = 4 - x 2 4 (hình vẽ). Diện tích của hình phẳng (H) bằng
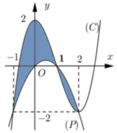
A. 2 4 π + 3 3
B. 4 π + 3 6
C. 4 3 + π 6
D. 4 π + 3 3
Cho hình phẳng (H) giới hạn bởi Parabol y = x 2 12 và đường cong có phương trình y = 4 - x 2 4 (hình vẽ). Diện tích của hình phẳng (H) bằng
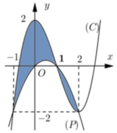
A. 2 4 π + 3 3
B. 4 π + 3 6
C. 4 3 + π 6
D. 4 π + 3 3
Cho hình phẳng (H) giới hạn bởi Parabol y = x 2 12 và đường cong có phương trình y = 4 − x 2 4 (hình vẽ). Diện tích của hình phẳng (H) bằng
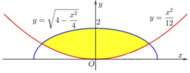
A. 2 4 π + 3 3
B. 4 π + 3 6
C. 4 3 + π 6
D. 4 π + 3 3
Cho hình phẳng (H) giới hạn bởi Parabol y = x 2 12 và đường cong có phương trình y = 4 - x 2 4 (hình vẽ). Diện tích của hình phẳng (H) bằng
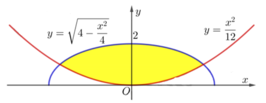
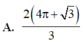
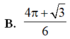
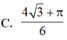
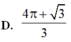
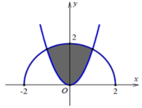
Cho (H) là hình phẳng giới hạn bởi parabol y = 3 x 2 và nửa đường tròn có phương trình y = 4 - x 2 với - 2 ≤ x ≤ 2 (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
A. 2 π + 5 3 3
B. 4 π + 5 3 3
C. 4 π + 3 3
D. 2 π + 3 3
Chọn D.
Hoành độ giao điểm của (P) và ( C) là nghiệm của 3 x 2 = 4 - x 2 <=> x = 1 hoặc x = -1
Khi đó, diện tích cần tính là H = 2x ( ∫ 0 1 4 - x 2 d x - ∫ 0 1 3 x 2 d x ) = 2 π + 3 3