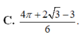Chọn đáp án A
Phương trình hoành độ giao điểm của parabol y = 3 2 x 2 và nửa đường elip
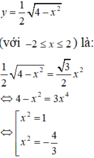
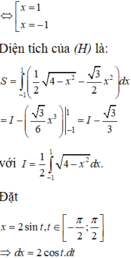
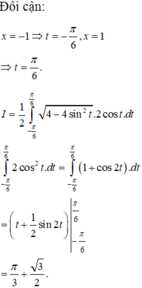
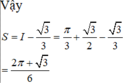
Chọn đáp án A
Phương trình hoành độ giao điểm của parabol y = 3 2 x 2 và nửa đường elip

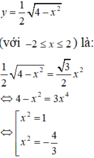
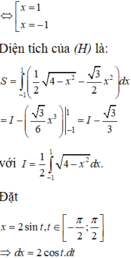
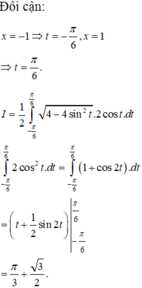
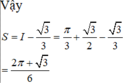
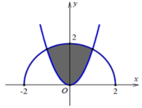
Cho (H) là hình phẳng giới hạn bởi parabol y = 3 x 2 và nửa đường tròn có phương trình y = 4 - x 2 với - 2 ≤ x ≤ 2 (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
A. 2 π + 5 3 3
B. 4 π + 5 3 3
C. 4 π + 3 3
D. 2 π + 3 3
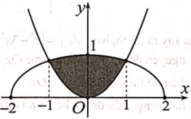
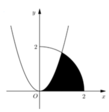
Cho (H) là hình phẳng giới hạn bởi parabol y = 3 x 2 cung tròn có phương trình y = 4 - x 2 (với 0 ≤ x ≤ 2 ) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
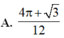
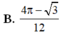
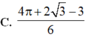
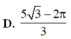
Thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi các đường: y = sin 2 / 3 x , y = 0 và x = π /2 bằng:
A. 1; B. 2/7;
C. 2 π ; D. 2 π /3.
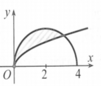
Cho (H) là hình phẳng giới hạn bởi đường cong y = x và nửa đường tròn có phương trình y = 4 - x 2 (với 0 £ x £ 4) (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
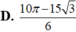
Cho (H) là hình phẳng được tô đậm trong hình vẽ được giới hạn bởi các đường có phương trình y = 10 3 x - x 2 , y = - x k h i x ≤ 1 x - 2 k h i x > 1 . Diện tích của (H) bằng
A. 11 2
B. 13 2
C. 11 6
D. 14 3
Diện tích hình phẳng giới hạn bởi parabol y= ( x - 2 ) 2 , đường cong y= x 3 và trục hoành bằng (phần tô đậm trong hình vẽ bên)
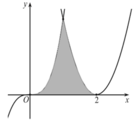
A. 11 2
B. 73 12
C. 7 12
D. 5 2
Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?
a) {y = x + sinx, y = x với 0 ≤ x ≤ π } và {y = x + sinx, y = x với π ≤ x ≤ 2 π }
b) {y = sinx, y = 0 với 0 ≤ x ≤ π } và {y = cosx, y = 0 với 0 ≤ x ≤ π };
c) {y = x , y = x 2 }
và { y = 1 - x 2 , y = 1 − x}
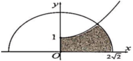
Cho (H) là hình phẳng giới hạn bởi parabol y = 1 4 x 2 + 1 với ( 0 ≤ x ≤ 2 2 ) nửa đường tròn y = 8 - x 2 và trục hoành, trục tung (phần tô đậm trong hình vẽ). Diện tích của (H) bằng:
![]()
![]()
![]()
![]()
Cho (H) là hình phẳng giới hạn bởi Parabol y = 3 x 2 cung tròn có phương trình y = 4 - x 2 và trục hoành (phần tô đậm trong hình vẽ). Diện tích của (H) bằng: