Cho lăng trụ đều ABC.A’B’C’ có cạnh đáy bằng 2a, diện tích xung quanh bằng 6 3 a 2 Thể tích của khối lăng trụ là
A. V=1/3 a 3
B. V=3/4 a 3
C. V= a 3
D. V=3 a 3
Cho lăng trụ đều ABC.A’B’C’ có cạnh đáy bằng 2a, diện tích xung quanh bằng 6 3 a 2 . Thể tích của khối lăng trụ là:
A. V= 1 3 a 3
B. V = 3 4 a 3
C. V= a 3
D. V = 3 a 3
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a và cạnh bên bằng 2a Một hình trụ có hai đáy là hai hình tròn ngoại tiếp hai tam giác ABC và A’B’C’ Diện tích xung quanh của hình trụ bằng
A. 4 3 π a 2 3
B. 2 3 π a 2 3
C. 4 π a 2
D. 2 π a 2
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có độ dài cạnh đáy bằng a và chiều cao bằng 2a. Tính thể tích V của khối cầu ngoại tiếp hình lăng trụ ABC.A’B’C’
A. 32 3 πa 3 27
B. 32 3 πa 3 9
C. 8 3 πa 3 27
D. 32 3 πa 3 81
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có độ dài cạnh đáy bằng a và chiều cao bằng 2a. Tính thể tích V của khối cầu ngoại tiếp hình lăng trụ ABC.A’B’C’.
A. V = 32 3 π a 3 27 .
B. V = 32 3 π a 3 9 .
C. V = 8 3 π a 3 27 .
D. V = 32 3 π a 3 81 .
Đáp án A.
Bán kính đường tròn đáy r = B C 2 sin A = a 3
Bán kính mặt cầu ngoại tiếp lăng trụ R = h 2 2 + r 2 = 2 a 3 ⇒ V = 4 3 π R 3 = 32 3 π a 3 27 .
Cho lăng trụ tam giác đều A B C . A ’ B ’ C ’ có cạnh đáy bằng 2a, O là trọng tâm tam giác ABC và A ' O = 2 a 6 3 . Thể tích của khối lăng trụ A B C . A ’ B ’ C ’ bằng
A. 2 a 3
B. 2 a 3 3 .
C. 4 a 3 3 .
D. 2 a 3 3 .
Phương pháp
Tính chiều cao lăng trụ dựa vào định lý Pytago
Tính thẻ tích lăng trụ V = S.h với S là diện tích đáy và h là chiều cao lăng trụ
Cách giải:
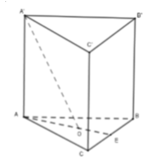
Gọi E là trung điểm của BC.

Chọn A
Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng 2a; O là trọng tâm tam giác ABC và A ' O = 2 6 a 3 Thể tích của khối lăng trụ ABC.A’B’C’ bằng
A. 2 a 3
B. 4 a 3 3
C. 2 a 3 3
D. 4 a 3
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều, các mặt bên đều là hình vuông. Biết rằng mặt cầu ngoại tiếp lăng trụ ABC.A’B’C’ có diện tích bằng 21ᴨ. Tính thể tích V của khối lăng trụ ABC.A’B’C’
A. V = 18
B. V = 27 3 4
C. V = 6
D. V = 9 3 4
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều, các mặt bên đều là hình vuông. Biết rằng mặt cầu ngoại tiếp lăng trụ ABC.A’B’C’ có diện tích bằng 21 π . Tính thể tích V của khối lăng trụ ABC.A’B’C’
![]()
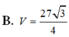
![]()
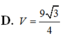
Câu 18: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, AA’ = 2a. Tính thể tích khối lăng trụ ABC.A’B’C’ theo a:
\(A,\sqrt{3a^3}\) \(B,\dfrac{\sqrt{3a^3}}{6}\) \(C,\dfrac{\sqrt{3a^3}}{2}\) \(D,2a^3\)
\(S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}.a.a\sqrt{3}=\dfrac{a^2\sqrt{3}}{2}\)
\(\Rightarrow V_{ABC}.A'B'C'=AA'.S_{ABC}=2a.\dfrac{a^2\sqrt{3}}{2}=a^3\sqrt{3}\)
Chọn A