Bài 1: Cho hàm số y=ax^2
a) Xác định a biết đồ thị của hàm số đi qua A(3;3)
b) Vẽ đồ thị hàm số vừa tìm được ở câu a
c) Tìm điểm thuộc đồ thị có tung độ bằng 1
Bài 2: Cho hai hàm số: y=x^2 (P) và y=2x (d)
a) vẽ đồ thị (P) và (d) của hai hàm số trên cùng một hệ trục tọa độ
b) Tìm tọa độ gioa điểm của (P) và (d)
Bài 3: Cho hai hàm số y= (m+1)x^2 và y= 2x-1.
Tìm m biết rằng đồ thị của hai hàm số cắt nhau tại điểm có hoành độ bằng 2

Đồ thị hàm số y = x 2 - x  và đồ thị hàm số y = 5 + 3 x  cắt nhau tại hai điểm A và B.  Khi đó, độ dài  AB  là:

A.  A B = 8 5

B.  A B = 25

C.  A B = 4 2

D.  A B = 10 2

Biết rằng đồ thị hàm số y = 2 x + 1 x  và đồ thị hàm số y = x 2 + x + 1  cắt nhau tại hai điểm, ký hiệu x 1 ; y 1 , x 2 , y 2  là tọa độ hai điểm đó. Tìm y 1 + y 2  

A.  y 1 + y 2 = 0

B.  y 1 + y 2 = 2

C.  y 1 + y 2 = 6

D.  y 1 + y 2 = 4

Biết rằng đồ thị hàm số  y = 2 x + 1 x và đồ thị hàm số y = x 2 + x + 1 cắt nhau tại hai điểm, kí hiệu  ( x 1 ; y 1 ) , ( x 2 ; y 2 ) là tọa độ hai điểm đó. Tính y 1 + y 2 .

A. y 1 + y 2 = 4 .

B. y 1 + y 2 = 6 .

C. y 1 + y 2 = 2 .

D. y 1 + y 2 = 0 .

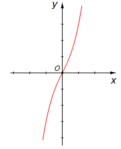
Cho hàm số f(x) = a x 4   +   b x 2   +   c ( a , b , c ∈ ℝ ,   a ≠ 0 ) có đồ thị (C). Biết rằng (C) không cắt trục Ox và đồ thị hàm số y = f''(x) cho bởi hình vẽ bên. Hàm số đã cho là hàm số nào trong các hàm số dưới đây?

A. y =  - 4 x 4 - x 2 - 1

B. y = 2 x 4 - x 2 + 2

C. y = x 4 + x 2 - 2

D. y = 1 4 x 4 + x 2 + 1