Cho số thức α sao cho phương trình 2 x - 2 - x = 2 cos α x có đúng 2019 nghiệm thực. Số nghiệm của phương trình 2 x + 2 - x = 4 + 2 cos α x là:
A. 2019
B. 2018
C. 4037
D. 4038
Cho phương trình ẩn \(x\): \(x^2-2\left(m-1\right)x-2=0\) (\(m\) là tham số). Tìm \(m\) để phương trình có 2 nghiệm phân biệt \(x_1\), \(x_2\) sao cho biểu thức: \(A=x_1^2+4x_2^2\) có giá trị nhỏ nhất.
\(\Delta=\left[-2\left(m-1\right)\right]^2-4.\left(-2\right)\)
\(=4m^2-8m+8+8\)
\(=4m^2-8m+16\)
\(=3m^2+\left(m-4\right)^2\)
Để pt có 2 nghiệm phân biệt thì \(\Delta>0\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\m>4\end{matrix}\right.\) \(\rightarrow m>4\)
Theo hệ thức Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m-2\left(1\right)\\x_1x_2=-2\end{matrix}\right.\)
\(A=x_1^2+4x_2^2\)
\(A=x_1^2+\left(2x_2\right)^2\)
\(\Rightarrow Min_A=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x_1=0\\x_2=0\end{matrix}\right.\)
Thế vào (1) ta được: \(0=2m-2\)
\(\Leftrightarrow m=1\)
Trong không gian Oxyz, cho mặt phẳng ( α ) có phương trình d 1 : x = 1 + 3 t y = 4 + t z = - 1 + 2 t , d 2 : x - 2 - 3 = y 2 = z - 4 - 2 .Phương trình đường thẳng ∆ nằm trong mặt phẳng ( α ) , cắt cả hai đường thẳng d 1 , d 2 là
A. x + 2 8 = y - 1 - 7 = z + 3 1
B. x - 2 - 8 = y + 1 7 = z - 3 - 1
C. x + 2 8 = y - 1 7 = z + 3 - 1
D. x - 2 - 8 = y 7 = z - 3 1
Tính khoảng cách giữa hai mặt phẳng (α) và (β) cho bởi các phương trình sau đây:
(α): x – 2 = 0
(β): x – 8 = 0.
Ta có (α)//(β)
Lấy M (8;0;0) ∈ (β)
d((α),(β)) = d(M,(α)) = 8 - 2 1 2 = 6
Cho phương trình \(x^2-2\left(m+1\right)x+m^2-3=0\)
Tìm m sao cho phương trình đã cho có 2 nghiệm phân biệt \(x_1;x_2\) thỏa mãn hệ thức \(x_1^2+x_2^2+3x_1x_2=14\)
\(\Delta'=\left(m+1\right)^2-\left(m^2-3\right)=2m+4>0\Rightarrow m>-2\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=m^2-3\end{matrix}\right.\)
\(x_1^2+x_2^2+3x_1x_2=14\)
\(\Leftrightarrow\left(x_1+x_2\right)^2+x_1x_2=14\)
\(\Leftrightarrow4\left(m+1\right)^2+m^2-3=14\)
\(\Leftrightarrow5m^2+8m-13=0\Rightarrow\left[{}\begin{matrix}m=1\\m=-\dfrac{13}{5}< -2\left(loại\right)\end{matrix}\right.\)
Để pt có 2 nghiệm phân biệt thì Δ'>0
Δ'= [-(m+1)]2-1*(m2-3)>0
= m2+2m+1-m2+3>0
= 2m+4 >0
↔ 2m>-4
↔ m>-2
áp dụng hệ thức vi-ét ta có :
[x1+x2=2(m+1)=2m+2
[x1x2=m2-3
ta lại có: x12+x22+3x1x2 =14
<=> (x1+x2)2+x1x2=14
<=> (2m+2)2 +(m2-3)=14
<=> 4m2+8m+4+m2-3-14=0
<=> 5m2+8m-17=0
Δ'=42-5(-17)
=101
Cho phương trình: x2 - 2(m-1)x + m2 - 3m = 0 (1) (x là ẩn số, m là tham số).
a. Giải phương trình (1) khi m = 0.
b. Tìm các giá trị của m để phương trình (1) có hai nghiệm sao cho biểu thức B= x12 + x22 +7 có giá trị nhỏ nhất.
Cho phương trình bậc hai: x2- 2(m+1)x + m2 + 4 =0 ( với m là tham số). Tìm m để phương trình có hai nghiệm x, x sao cho biểu thức P = x1 + x2 - x1x2 đạt giá trị lớn nhất và tìm giá trị lớn nhất đó.
\(\Delta^'=b^'^2-ac=\left(m+1\right)^2-\left(m^2+4\right)=2m-3\ge0\Rightarrow m\ge\frac{3}{2}\)(1)
Và\(x_1;x_2\)thỏa mãn:\(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=2\left(m+1\right)\\x_1x_2=\frac{c}{a}=m^2+4\end{cases}}\)Do đó \(P=x_1+x_2-x_1x_2=2\left(m+1\right)-\left(m^2+4\right)=-m^2+2m-2\)\(=-\left(m^2-2m+1\right)-1=-\left(m-1\right)^2-1\)(với \(m\ge\frac{3}{2}\))
Ta lại có với \(m\ge\frac{3}{2}\)tức là \(m-1\ge\frac{1}{2}>0\)thì hàm số \(P\left(m\right)=-\left(m-1\right)^2-1\)là nghịch biến trong khoảng [\(\frac{3}{2};+\infty\)); tức là P lớn nhất khi m nhỏ nhất. Vậy khi m nhỏ nhất bằng \(\frac{3}{2}\)thì phương trình đã cho có 2 nghiệm \(x_1=x_2=\frac{5}{2}\)và P đạt giá trị lớn nhất = \(-\frac{5}{4}\).\(\Delta'=\left(m-1\right)^2-m^2-4\)
\(\Delta'=m^2-2m-m^2+1-4\)
\(\Delta'=-2m-3\)
Để pt có 2 nghiệm phân biệt \(\Rightarrow\)\(\Delta'\ge0\)\(\Rightarrow-2m-3\ge0\)
\(\Leftrightarrow m\le-\frac{3}{2}\)
Theo vi-ét\(\Rightarrow\hept{\begin{cases}x_1+x_2=2\left(m+1\right)\\x_1x_2=m^2+4\end{cases}}\)
\(P=x_1+x_2-x_1x_2\)
\(P=2m+1-m^2-4\)
\(P=-m^2+2m-3\)
\(P=\left(1-m\right)^2-2\)
\(\left(1-m\right)^2-2\ge-2\Rightarrow P\ge-2\)
MIN \(P=-2\)khi\(m=1\)
MAX \(P=\frac{-1}{2}\)khi \(m=\frac{5}{4}\)
Trong không gian tọa độ Oxyz cho đường thẳng có phương trình x - 1 2 = y + 1 - 1 = z 2 và mặt phẳng α có phương trình x+y-z-2=0. Tính côsin của góc tạo bởi đường thẳng ∆ và mặt phẳng α
![]()
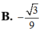
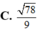
![]()
Trong không gian tọa độ Oxyz cho đường thẳng △ có phương trình x - 1 2 = y + 1 - 1 = z 2 và mặt phẳng ( α ) có phương trình x+y-z-2=0 Tính côsin của góc tạo bởi đường thẳng △ và mặt phẳng ( α )
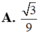
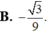
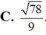
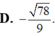
Cho phương trình: x2 + (m+2)x - 8 = 0, với m la tham số>
a) Giải phương trình khi m=4.
b)Tìm tất cả các giá trị m để phương tình có 2 nghiệm x1,x2 sao cho biểu thức Q= (x12 -1)(x22 - 4) có giá trị lớn nhất.