Biết bán kính B 0 là r 0 = 5 , 3 . 10 - 11 m . Bán kính quỹ đạo dừng N trong nguyên tử hiđrô bằng
A. 84 , 8 . 10 - 11 m
B. 21 , 2 . 10 - 11 m
C. 26 , 5 . 10 - 11 m
D. 132 , 5 . 10 - 11 m
Cho mặt cầu (S) có đường kính là AB biết rằng A(6; 2; -5), B(-4; 0; 7) Tìm tọa độ tâm I và bán kính r của mặt cầu (S).
Tâm của mặt cầu (S) là trung điểm I (1; 1; 1) của đoạn thẳng AB và bán kính của mặt cầu (S) là R = IA = √62
Trong nguyên tử hidro, với r0 là bán kính Bo thì bán kính quỹ đạo dừng của êlectron không thể là
A.12r0.
B.25r0.
C.9r0.
D.16r0.
Trong nguyên tử hydro, bán kính quỹ đạo dừng của electron là
\(r_n=n^2.r_0;n\in N^*\)
=> không thể có \(r = 12.r_0\) được.
bán kính quỹ đạo = r0 x bình phương 1 số nguyên (1,2,3,4,....)
Đáp án A
a) Tính chu vi hình tròn biết bán kính r = 4,25 dm.
b) Tính chu vi hình tròn biết đường kính d = 4/5 m.
c) Tính bán kính của hình tròn biết chu vi C = 9,42m.
d) Tính chu vi hình tròn biết diện tích của hình tròn là 12,56 m2
giúp mình nhanh nhé đang gấp!
Trong mặt phẳng toạ độ Oxy, nêu mối liên hệ giữa x và y để:
a) Điểm M(x ; y) nằm trên đường tròn tâm O(0 : 0) bán kính 5.
b) Điểm M(x ; y) nằm trên đường tròn (C) tâm I(a; b) bán kính R.
a) Mối liên hệ giữa x và y là: \({x^2} + {y^2} = 5\)
b) Mối liên hệ giữa x và y là: \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\)
Bài 10:Cho ABC có a = 8, b =10, c =13 a. ABC có góc tù hay không ? Tính bán kính đường tròn ngoại tiếp ABC. b. Tính diện tích ABC
Bài 11:Cho tam giác ABC có: a = 6, b = 7, c = 5. a) Tính S ,h ,R,r ABC a b) Tính bán kính đường tròn đi qua A, C và trung điểm M của cạnh AB.
Bài 12:Cho tam giác ABC có: AB = 6, BC = 7, AC = 8. M trên cạnh AB sao cho MA = 2 MB. a) Tính các góc của tam giác ABC. b) Tính S ,h ,R ABC a , r. c) Tính bán kính đường tròn ngoại tiếp ∆MBC.
Bài 13:Cho ABC có 0 0 A B b = = = 60 , 45 , 2 tính độ dài cạnh a, c, bán kính đường tròn ngoại tiếp và diện tích tam giác ABC
Bài 14:Cho ABC AC = 7, AB = 5 và 3 cos 5 A = . Tính BC, S, a h , R, r.
Bài 15:Cho ABC có 4, 2 m m b c = = và a =3 tính độ dài cạnh AB, AC.
Bài 16:Cho ABC có AB = 3, AC = 4 và diện tích S = 3 3 . Tính cạnh BC
Bài 17:Cho tam giác ABC có ˆ o A 60 = , c h 2 3 = , R = 6. a) Tính độ dài các cạnh của ∆ABC. b) Họi H là trực tâm tam giác ABC. Tính bán kính đường tròn ngoại tiếp ∆AHC.
Bài 18:a. Cho ABC biết 0 0 a B C = = = 40,6; 36 20', 73 . Tính BAC , cạnh b,c. b.Cho ABC biết a m = 42,4 ; b m = 36,6 ; 0 C = 33 10' . Tính AB, và cạnh c.
Bài 19:Tính bán kính đường tròn nội tiếp ABC biết AB = 2, AC = 3, BC = 4.
Bài 20:Cho ABC biết A B C (4 3; 1 , 0;3 , 8 3;3 − ) ( ) ( ) a. Tính các cạnh và các góc của ABC b. Tính chu vi và diện tích ABC
Điền vào ô trống trong bảng sau (S là diện tích hình tròn có bán kính R)
| R | 0 | 1 | 2 | 3 | 4 | 5 | 10 | 20 |
| S |
| R | 0 | 1 | 2 | 3 | 4 | 5 | 10 | 20 |
| S | 0 | π | 4π | 9π | 16π | 25π | 100π | 400π |
Trong nguyên tử Hiđrô, bán kính Bo là r 0 = 5 , 3 . 10 - 11 m . Bán kính quỹ đạo dừng của trạng thái kích thích thứ 3 là:
A. 132 , 5 . 10 - 11 m .
B. 21 , 2 . 10 - 11 m .
C. 84 , 8 . 10 - 11 m .
D. 47 , 7 . 10 - 11 m
- Trạng thái kích thích thứ 3 ứng với quỹ đạo dừng N (K,L,M,N).
- Tức là n = 4. Vậy bán kính là :
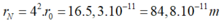
Trên đường tròn tâm O bán kính R lấy hai điểm A và B sao cho AB = R. Số đo góc
AOB chắn cung nhỏ AB có số đo là :
A.30 0 B. 60 0 C. 90 0 D . 120 0
AOB=60 độ ( OA=OB=AB=R -> OAB là tam giác đều)
Trong không gian Oxyz, cho mặt cầu (S) có phương trình x 2 + y 2 + z 2 - 2 x + 6 y + 8 z - 599 = 0 . Biết rằng mặt phẳng ( α ) : 6 x - 2 y + 3 z + 49 = 0 cắt (S) theo giao tuyến là đường tròn (C) có tâm là điểm P (a;b;c) và bán kính đường tròn (C) là r. Giá trị của tổng S = a+b+c+r là
A. S = 11.
B. S = 13.
C. S = 37.
D. S = -13
Trong không gian Oxyz, cho mặt cầu (S) có phương trình
S : x 2 + y 2 + z 2 - 2 x + 6 y + 8 z - 599 = 0 .
Biết rằng mặt phẳng α : 6x-2y+3z+49=0 cắt (S) theo giao tuyến là đường tròn (C) có tâm là điểm P(a;b;c) và bán kính đường tròn (C) là r. Giá trị của tổng S = a+b+c+r là
A. -13
B. 37
C. 11
D. 13