Cho x, y là hai số thực tùy ý, tìm giá trị nhỏ nhất của biểu thức sau: P = x 2 + 5 y 2 + 4 x y + 6 x + 16 y + 32

Những câu hỏi liên quan
cho x,y là hai số thực tùy ý , tìm giá trị nhỏ nhất của biểu thức sau
\(P=x^2+5y^2+4xy+6x+16y+32\)
Có P = x2 + 5y2 + 4xy + 6x + 16y + 32
= [(x2 + 4xy + 4y2) + 6x + 12y + 9] + (y2 + 4y + 22) + 19
= [(x + 2y)2 + 2(x + 2y).3 + 32 ] + (y + 2)2 + 19
= (x + 2y + 3)2 + (y + 2)2 + 19
Thấy (x + 2y + 3)2 ≥ 0 với mọi x; y
(y + 2)2 ≥ 0 với mọi y
=> (x + 2y + 3)2 + (y + 2)2 ≥ 0 với mọi x; y
=> (x + 2y + 3)2 + (y + 2)2 + 19 ≥ 19 với mọi x; y
=> P ≥ 19 với mọi x; y
Dấu "=" xảy ra khi x + 2y + 3 = 0 và y + 2 = 0
Bn tự giải tiếp nha, mk ko biết có nhầm chỗ nào ko nhưng cách lm như vậy đó
cho x,y là hai số thực tùy ý , tìm giá trị nhỏ nhất của biểu thức
p=3x^2+3y^2+4xy+2x-2y+2020
Bạn có ghi nhầm đề không vậy?
Cho x , y là các số thực tùy ý. Tìm giá trị nhỏ nhất của biểu thức:
A = x\(^2\) + 2y\(^2\) + 2xy - 2\(\sqrt{2}\)x - 2(\(\sqrt{2}\) + 1)y +2022
Lời giải:
$A=(x^2+2xy+y^2)+y^2-2\sqrt{2}(x+y)-2y+2022$
$=(x+y)^2-2\sqrt{2}(x+y)+2+(y^2-2y+1)+2019$
$=(x+y-\sqrt{2})^2+(y-1)^2+2019$
$\geq 2019$
Vậy $A_{\min}=2019$. Giá trị này đạt tại $x+y-\sqrt{2}=y-1=0$
$\Leftrightarrow y=1; x=\sqrt{2}-1$
Đúng 0
Bình luận (0)
Cho X và Y là 2 số thực tuỳ ý , tìm giá trị nhỏ nhất của biểu thức sau :
A= x2+5y2+4xy+6x+16y+32
Lời giải:
$A=(x^2+4y^2+4xy)+y^2+6x+16y+32$
$=(x+2y)^2+6(x+2y)+(y^2+4y)+32$
$=(x+2y)^2+6(x+2y)+9+(y^2+4y+4)+19$
$=(x+2y+3)^2+(y+2)^2+19\geq 0+0+19=19$
Vậy $A_{\min}=19$. Giá trị này đạt tại $x+2y+3=y+2=0$
$\Leftrightarrow y=-2; x=1$
Đúng 1
Bình luận (2)
Cho x, y, z là những số thực tùy ý. Tìm giá trị lớn nhất, nhỏ nhất của hàm số sau trên tập xác định của nó :
\(y=\sqrt{x-1}+\sqrt{5-x}\)
- Áp dụng BĐT Bunhia- Cốp xki ta có:
\(\left(\sqrt{x-1}+\sqrt{5-x}\right)^2\le\left(1^2+1^2\right)\left(x-1+5-x\right)\)\(=2.4=8\).
Suy ra: \(\sqrt{x-1}+\sqrt{5-x}\le2\sqrt{2}\).
Vậy max \(\sqrt{x-1}+\sqrt{5-x}=2\sqrt{2}\) khi:
\(\sqrt{x-1}=\sqrt{5-x}\)\(\Leftrightarrow x-1=5-x\)\(\Leftrightarrow x=3\).
- Ta có: \(\sqrt{x-1}+\sqrt{5-x}\ge\sqrt{x-1+5-x}=\sqrt{4}=2\).
Vậy GTNN của \(\sqrt{x-1}+\sqrt{5-x}=2\) khi:
\(\left[{}\begin{matrix}x-1=0\\5-x=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\).
Đúng 0
Bình luận (0)
Cho x,y là hai số thực thỏa mãn (x+y)\(^2\)+7x+7y+y\(^2\)+6=0.Tìm giá trị nhỏ nhất,giá trị lớn nhất của biểu thức M=x+y+1
Ta có : (x+y)2+7x+7y+y2+6=0
( x2 + y2 + \(\frac{49}{4}\)+ 7x + 7y + 2xy ) + y2 - \(\frac{25}{4}\)= 0
( x + y + \(\frac{7}{2}\))2 = \(\frac{25}{4}\)- y2 \(\le\frac{25}{4}\)
\(\Rightarrow\frac{-5}{4}\le x+y+\frac{7}{2}\le\frac{5}{4}\)
\(\Rightarrow\frac{-15}{4}\le x+y+1\le\frac{-5}{4}\)
\(\Rightarrow\)......
Đúng 0
Bình luận (0)
lon so roi,
thay -5/4 thành -5/2 ; 5/4 thành 5/2
-15/4 thành -5 ; 5/2 thành 0
Đúng 0
Bình luận (0)
chị còn cách nữa
nhưng hình như nó dài hơn ấy
thôi em dùng cách tren cx đc
Đúng 0
Bình luận (0)
Cho biểu thức P=x2+y2 với x,y là hai số thực thay đổi nhưng luôn thỏa mãn x+y+xy=15. tìm giá trị nhỏ nhất của biểu thức P
Ta có: \(15=x+y+xy\le x+y+\frac{\left(x+y\right)^2}{4}\Rightarrow\frac{t^2}{4}+t\ge15\)(\(t=x+y\))
\(\Leftrightarrow\left(t-6\right)\left(t+10\right)\ge0\Leftrightarrow\orbr{\begin{cases}t\ge6\\t\le-10\end{cases}}\)
\(P=x^2+y^2=\frac{1}{2}.2\left(x^2+y^2\right)\ge\frac{1}{2}\left(x+y\right)^2\ge\frac{1}{2}.6^2=18\)
Dấu \(=\)xảy ra khi \(x=y=3\).
Cho x,y là các số thực. Tìm giá trị nhỏ nhất của biểu thức P = \(\left(x+2y+1\right)^2+\left(x+2y+5\right)^2\)
Đặt \(x+2y+1=a\)
\(P=a^2+\left(a+4\right)^2=2a^2+8a+16=2\left(a+2\right)^2+8\ge8\)
Đúng 2
Bình luận (1)
Cho hai số thực x, y thỏa mãn
0
≤
x
≤
1
2
,
0
y
≤
1
và
log
11
−
2
x
−
y
2
y...
Đọc tiếp
Cho hai số thực x, y thỏa mãn 0 ≤ x ≤ 1 2 , 0 < y ≤ 1 và log 11 − 2 x − y = 2 y + 4 x − 1. Xét biểu thức P = 16 x 2 y − 2 x 3 y + 2 − y + 5. Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của P. Khi đó giá trị của biểu thức T = 4m + M bằng bao nhiêu?
A. 16
B. 18
C. 17
D. 19
Đáp án C
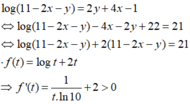
Suy ra f(t) đồng biến trên TXĐ và pt f(t) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 − 2 x − y = 10 ⇒ y = 1 − 2 x ⇒ P = 16 x 2 ( 1 − 2 x ) − 2 x ( 3 − 6 x + 2 ) − 1 + 2 x + 5 = − 32 x 3 + 28 x 2 − 8 x + 4 P ' = − 96 x 2 + 56 x − 8 P ' = 0 ⇔ x = 1 4 x = 1 3 P ( 0 ) = 4 , P ( 1 3 ) = 88 27 , P ( 1 4 ) = 13 4 , P ( 1 2 ) = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17
Đúng 0
Bình luận (0)


















