3:

góc C=90-50=40 độ

Xét ΔABC vuông tại A có sin C=AB/BC

=>4/BC=sin40

=>\(BC\simeq6,22\left(cm\right)\)

\(AC=\sqrt{BC^2-AB^2}\simeq4,76\left(cm\right)\)

1:

góc C=90-60=30 độ

Xét ΔABC vuông tại A có

sin B=AC/BC

=>3/BC=sin60

=>\(BC=\dfrac{3}{sin60}=2\sqrt{3}\left(cm\right)\)

=>\(AB=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)

\(\widehat{C}=90-\widehat{B}=90-38=52\)

AC=\(\sin B.BC=\sin38.8\approx4,92cm\)

AB=\(\cos B.BC=\cos38.8\approx6,3cm\)

a)Theo đề: BC/B'C'=10/5=1/2

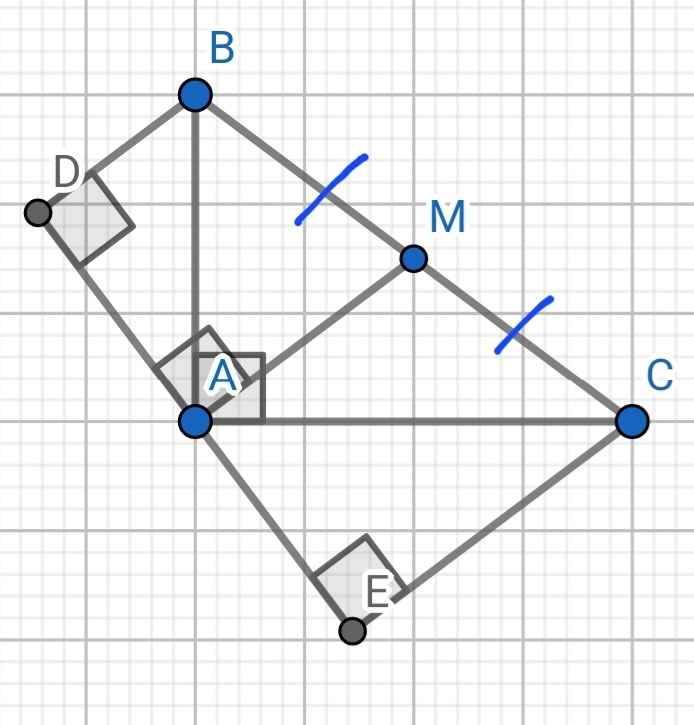
a) Sửa đề: Chứng minh ∆ABC ∽ ∆EAC

Giải:

∆ABC vuông tại A

⇒ BC² = AB² + AC² (Pytago)

= 6² + 8²

= 100

⇒ BC = 10 (cm)

Do AM là đường trung tuyến ứng với cạnh huyền BC

⇒ AM = BM = CM = BC : 2

= 10 : 2 = 5 (cm)

∆AMC có AM = CM = 5 (cm)

⇒ ∆AMC cân tại M

⇒ ∠MAC = ∠MCA (hai góc ở đáy)

Do MA ⊥ DE (gt)

CE ⊥ DE (gt)

⇒ MA // DE

⇒ ∠MAC = ∠ACE (so le trong)

Mà ∠MAC = ∠MCA (cmt)

⇒ ∠MAC = ∠ACE

⇒ ∠ACE = ∠BCA (do ∠MAC = ∠BAC)

Xét hai tam giác vuông:

∆ABC và ∆EAC có:

∠BCA = ∠ACE (cmt)

⇒ ∆ABC ∽ ∆EAC (g-g)

b) Do ∆ABC ∽ ∆EAC (cmt)

⇒ AC/CE = BC/AC

⇒ CE = AC²/BC

= 8²/10

= 6,4 (cm)

Câu 1: B

Câu 2:Sửa đề: \(AD^2=DE^2+AE^2\)

=> Chọn A

Câu 3: Chọn D

Câu 4: \(EF=3\sqrt{2}cm\)

Câu 1 là 70 bạn nhé

a, Áp dụng định lí Pytago cho tam giác ABC vuông tại A

\(AB^2+AC^2=BC^2\Rightarrow BC^2=\left(\frac{3}{5}BC\right)^2+AC^2\)

\(\Leftrightarrow AC^2=\frac{16}{25}BC^2\Leftrightarrow AC=\frac{4}{5}BC\)

* Áp dụng hệ thức : 

\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Rightarrow\frac{1}{144}=\frac{1}{\frac{9}{25}BC^2}+\frac{1}{\frac{16}{25}BC^2}\)

\(\Leftrightarrow\frac{1}{144}=\frac{\frac{16}{25}BC^2+\frac{9}{25}BC^2}{\frac{16}{25}BC^2.\frac{9}{25}BC^2}\Rightarrow144BC^2=\frac{144}{625}BC^4\)

\(\Leftrightarrow\frac{144}{625}BC^2-144=0\Leftrightarrow BC^2=144.\frac{625}{144}=625\Leftrightarrow BC=25\)cm 

\(\Rightarrow AB=\frac{3}{5}BC=\frac{3}{5}.25=\frac{75}{5}=15\)cm

\(\Rightarrow AC=\frac{4}{5}BC=\frac{4}{5}.25=\frac{100}{5}=20\)

Chu vi tam giác là : \(P_{ABC}=AB+BC+AB=15+20+25=60\)cm²

b, Vì AD là phân giác nên : \(\frac{AB}{AC}=\frac{BD}{DC}=\frac{15}{20}=\frac{3}{4}\Rightarrow AB=\frac{3}{4}AC\)

Lại có : \(BC=BD+DC=15+20=35\)cm 

Áp dụng định lí Pytago cho tam giác ABC vuông tại A

\(BC^2=AC^2+AB^2=AC^2+\left(\frac{3}{4}AC\right)^2\)

\(\Rightarrow\frac{25}{16}AC^2=1225\Leftrightarrow AC^2=\frac{16.1225}{25}=784\Leftrightarrow AC=28\)cm 

\(\Rightarrow AB=\frac{3}{4}.28=21\)cm 

* Áp dụng hệ thức : \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Rightarrow\frac{1}{AH^2}=\frac{AC^2+AB^2}{AB^2AC^2}\)

\(\Leftrightarrow\frac{1}{AH^2}=\frac{784+441}{345744}\Leftrightarrow1225AH^2=345744\Leftrightarrow AH^2=\frac{7056}{25}\Leftrightarrow AH=\frac{84}{5}\)cm 

* Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{441}{35}=\frac{63}{5}\)cm 

\(\Rightarrow HD=BD-BH=15-\frac{63}{5}=\frac{12}{5}\)cm

Áp dụng định lí Pytago cho tam giác AHD vuông tại H 

\(AD^2=AH^2+HD^2=\left(\frac{84}{5}\right)^2+\left(\frac{12}{5}\right)^2=288\Rightarrow AD=12\sqrt{2}\)cm