a. Hàm số y = -2x + 1 có đồ thị là đường thẳng => Không có cực trị  ( điều này hiển nhiên )

b) \(y=f\left(x\right)=\frac{x}{3}\left(x-3\right)^2\)

Có: 

\(y'=f'\left(x\right)=\frac{1}{3}.\left(x-3\right)^2+\frac{x}{3}.2.\left(x-3\right)=\frac{1}{3}\left(x-3\right)\left(x-3+2x\right)=\left(x-3\right)\left(x-1\right)\)

\(f''\left(x\right)=x-1+x-3=2x-4\)

+) \(f'\left(x\right)=0\Leftrightarrow\orbr{\begin{cases}x=3\\x=1\end{cases}}\)

+) Với x =3 có: \(f''\left(3\right)=2.3-4=2>0\)=> y = f ( x ) đạt cực tiểu tại x = 3.

+ Với x = 1 có: \(f''\left(1\right)=2.1-4=-1< 0\)=> y = f ( x ) đạt cực đại tại x =1

Còn có nhiều cách khác nữa: Vẽ đồ thị, vẽ bảng biến thiên,...

hay vải chưởng đè sai mà bn vẫn làm được

Ta biết hàm số y = f(x) có cực trị khi phương trình y’ = 0 có nghiệm và y’ đổi dấu khi qua các nghiệm đó.

Ta có:

Xét y’ = 0, ta có: y′ = 3 x 2  − 2mx + (m – 2/3)

∆ ’ > 0 khi m < 1 hoặc m > 2 (∗)

Để hàm số có cực trị tại x = 1 thì

y′(1) = 3 − 2m + m – 2/3 = 0 ⇔ m = 7/3, thỏa mãn điều kiện (∗)

Với m = 7/3 thì hàm số đã cho trở thành:

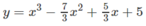
Ta có:

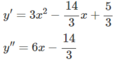
Vì y′′(1) = 6 – (14/3) > 0 nên hàm số đạt cực tiểu tại x = 1 và y CT  = y(1) = (16/3).

Ta biết hàm số y = f(x) có cực trị khi phương trình y’ = 0 có nghiệm và y’ đổi dấu khi qua các nghiệm đó.

Ta có:

Xét y’ = 0, ta có: y′ = 3 x 2  − 2mx + (m – 2/3)

Δ’ > 0 khi m < 1 hoặc m > 2 (∗)

Để hàm số có cực trị tại x = 1 thì

y′(1) = 3 − 2m + m – 2/3 = 0 ⇔ m = 7/3, thỏa mãn điều kiện (∗)

Với m = 7/3 thì hàm số đã cho trở thành:

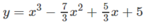
Ta có:

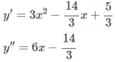
Vì y′′(1) = 6 – (14/3) > 0 nên hàm số đạt cực tiểu tại x = 1 và y C T  = y(1) = (16/3).

\(y=x^3-3mx^2+\left(m-1\right)x+2\)

\(y'=3x^2-6mx+m-1\)

\(y''=6x-6=6\left(x-1\right)\)

Để hàm số trên đạt cực trị tại \(x_o=2\) khi và chỉ khi

\(\left\{{}\begin{matrix}y'\left(2\right)=0\\y''\left(2\right)>0\end{matrix}\right.\) \(\)

\(\Leftrightarrow\left\{{}\begin{matrix}12-12m+m-1=0\\6\left(2-1\right)=6>0\left(luôn.đúng\right)\end{matrix}\right.\)

\(\Leftrightarrow11m=11\)

\(\Leftrightarrow m=1\)

Vậy với \(m=1\) thỏa yêu cầu đề bài.

a) y′ = 3 x 2  + 2(m + 3)x + m

y′ = 0 ⇔ 3 x 2  + 2(m + 3)x + m = 0

Hàm số đạt cực trị tại x = 1 thì:

y′(1) = 3 + 2(m + 3) + m = 3m + 9 = 0 ⇔ m = −3

Khi đó,

y′ = 3 x 2  – 3;

y′′ = 6x;

y′′(1) = 6 > 0;

Suy ra hàm số đạt cực tiểu tại x = 1 khi m = 3.

b) y′ = −( m 2  + 6m) x 2  − 4mx + 3

y′(−1) = − m 2  − 6m + 4m + 3 = (− m 2  − 2m – 1) + 4 = −(m + 1)2 + 4

Hàm số đạt cực trị tại x = -1 thì :

y′(−1) = − ( m + 1 ) 2  + 4 = 0 ⇔ ( m + 1 ) 2  = 4

⇔ 

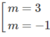
Với m = -3 ta có y’ = 9 x 2  + 12x + 3

⇒ y′′ = 18x + 12

⇒ y′′(−1) = −18 + 12 = −6 < 0

Suy ra hàm số đạt cực đại tại x = -1.

Với m = 1 ta có:

y′ = −7 x 2  − 4x + 3

⇒ y′′ = −14x − 4

⇒ y′′(−1) = 10 > 0

Suy ra hàm số đạt cực tiểu tại x = -1

Kết luận: Hàm số đã cho đạt cực đại tại x = -1 khi m = -3.

\(y'=3x^2-2mx+2\left(m+1\right)\)

\(y''=6x-2m\)

Hàm đạt cực tiểu tại \(x=-1\) khi:

\(\left\{{}\begin{matrix}y'\left(-1\right)=0\\y''\left(-1\right)>0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}3+2m+2\left(m+1\right)=0\\-6-2m>0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m=-\dfrac{5}{4}\\m< -3\end{matrix}\right.\) \(\Rightarrow\) không tồn tại m thỏa mãn