Cho hàm số y=2x+4 có đồ thị là(d)
a) Vẽ đồ thị của hàm số
b) Tính góc tạo bởi(d) và trục Ox

Những câu hỏi liên quan
Bài 2: : Cho hàm số y= -2x +8
a. Vẽ đồ thị hàm số
b. Tính góc tạo bởi đồ thị hàm số với trục ox?
c. Tính khoảng cách từ gốc tọa độ đến đồ thị hàm số?
d. Điểm A(-1; 10 ) có thuộc đồ thị hàm số không?
e. Tính diện tích và chu vi của hình tạo bởi đồ thị hàm số với hai
trục tọa độ?
Cho hàm số y=2x 4 có đồ thị là(d) a) Vẽ đồ thị của hàm số b) Tính góc tạo bởi(d) và trục Ox
cho hàm số y=2x-4 có đồ thị là (d)
a)vẽ đồ thị (d) của hàm số
b)tìm toạ độ giao điểm m của (d) và đường thẳng y=8-x bằng phép tính
c)tính góc tạo bởi đường thẳng y=2x-4 với trục Ox
mấy bạn làm giúp ạ, mình đang cần gấp:(
b,Phương trình hoành độ:
2x-4=8-x
<=>x=4
=>y=2x-4=8-4=4
hok tốt
Đúng 1
Bình luận (2)
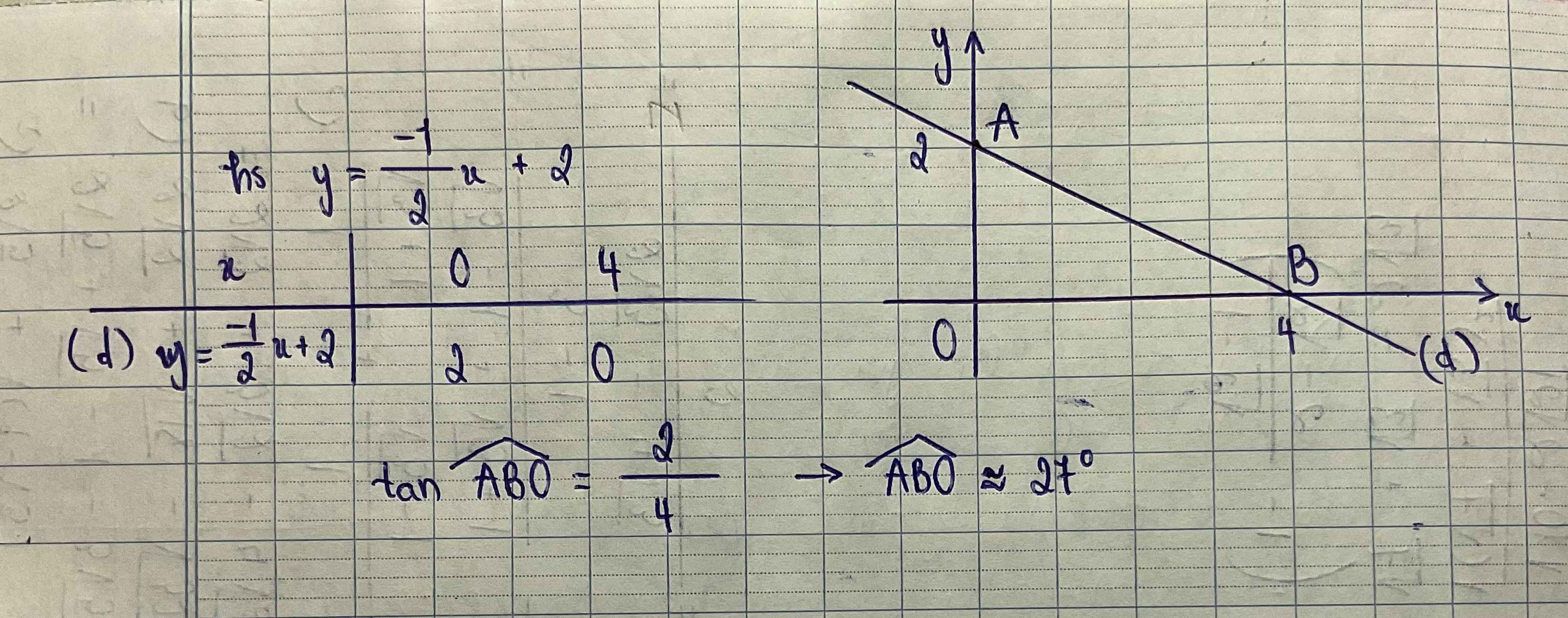
Cho hàm số có đồ thị (d): -1/2x+2
a. Vẽ đồ thị hàm số
b. Gọi A và B thứ tự là giao điểm của (d) với trục tung và trục hoành,Tính góc ABO
Cho hàm số y= 2x-3 có đồ thị (D)
a) Vẽ đồ thị (D)
b)Tính khoảng cách từ gốc tọa độ đến (D)
c) Tính góc a tạo bởi đường thẳng (D) và trục Ox.(Làm tròn đến phút)
cho 2 hàm số y=-2x+5 ; y=0.5x
a vẽ đô thị hàm số
b tìm tọa độ giao điểm của 2 đô thị
c tính góc tạo bởi D với trục Ox
Cho hai hàm số y= -2x+5(d) và y =0.5x(d')
a) Vẽ đthi d và d' của 2 hàm số trên mặt phẳng tọa độ
b) Tính góc α tạo bởi đường thẳng d và trục Ox
c)Gọi gđiểm của d với trục Oy là A Tính P và S của tam giác MOA
____________________
a) vẽ đths (d) và (d')
y = -2x + 5 (d) : x = 0 => y = 5
y = 0 => x = 2,5
y = 0,5x : x = 2 => y = 1
b) tanα = 5/2,5 = 2
=> α = 63độ 26'
c) P = 5 + 2,5 + √(5^2 + 2,5^2) = 7,5+ 5√5/2
S = 1/2.5.2,5 = 1
a) Vẽ đthi d và d' của 2 hàm số trên mặt phẳng tọa độ
b) Tính góc α tạo bởi đường thẳng d và trục Ox
c)Gọi gđiểm của d với trục Oy là A Tính P và S của tam giác MOA
____________________
a) vẽ đths (d) và (d')
y = -2x + 5 (d) : x = 0 => y = 5
y = 0 => x = 2,5
y = 0,5x : x = 2 => y = 1
b) tanα = 5/2,5 = 2
=> α = 63độ 26'
c) P = 5 + 2,5 + √(5^2 + 2,5^2) = 7,5+ 5√5/2
S = 1/2.5.2,5 = 1

Đúng 0
Bình luận (0)
Cho hàm số bậc nhất y-2x -5 (d) và y -x (d)
A. Vẽ đồ thị d và d của 2 hàm số đã cho trêb cùng 1 hệ tọa đọi Oxy
B. Tìm tọa độ điểm M là giao điểm của 2 đồ thị vừa vẽ ( bằng phép tính)
C. Tính góc alpha tạo bởi đường thẳng d với trục hoành Ox ( làm tròn kết quả đến độ)
D. Gọi giao điểm của d với trục Oy là A, tính chu vi và diện tích tam giác MOA ( đơn vị đo trên các trục tọa độ là cm)
Đọc tiếp
Cho hàm số bậc nhất y=-2x -5 (d) và y= -x (d') A. Vẽ đồ thị d và d' của 2 hàm số đã cho trêb cùng 1 hệ tọa đọi Oxy B. Tìm tọa độ điểm M là giao điểm của 2 đồ thị vừa vẽ ( bằng phép tính) C. Tính góc alpha tạo bởi đường thẳng d với trục hoành Ox ( làm tròn kết quả đến độ) D. Gọi giao điểm của d với trục Oy là A, tính chu vi và diện tích tam giác MOA ( đơn vị đo trên các trục tọa độ là cm)
a) \(\left\{{}\begin{matrix}\left(d\right):y=-2x-5\\\left(d'\right):y=-x\end{matrix}\right.\)
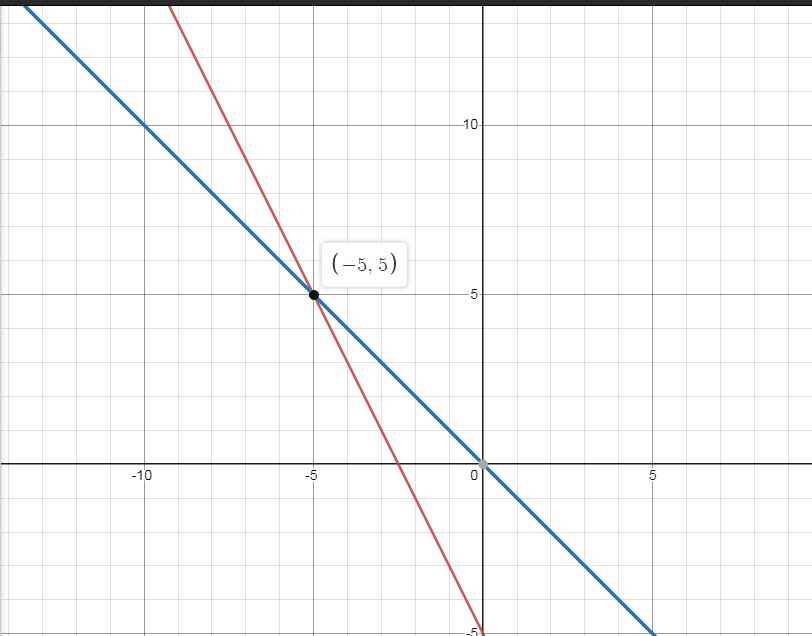
b) \(\left(d\right)\cap\left(d'\right)=M\left(x;y\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-2x-5\\y=-x\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x=-2x-5\\y=-x\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-5\\y=5\end{matrix}\right.\)
\(\Rightarrow M\left(-5;5\right)\)
c) Gọi \(\widehat{M}=sđ\left(d;d'\right)\)
\(\left(d\right):y=-2x-5\Rightarrow k_1-2\)
\(\left(d'\right):y=-x\Rightarrow k_1-1\)
\(tan\widehat{M}=\left|\dfrac{k_1-k_2}{1+k_1.k_2}\right|=\left|\dfrac{-2+1}{1+\left(-2\right).\left(-1\right)}\right|=\dfrac{1}{3}\)
\(\Rightarrow\widehat{M}\sim18^o\)
Đúng 0
Bình luận (0)
d) \(\left(d\right)\cap Oy=A\left(0;y\right)\)
\(\Leftrightarrow y=-2.0-5=-5\)
\(\Rightarrow A\left(0;-5\right)\)
\(OA=\sqrt[]{0^2+\left(-5\right)^2}=5\left(cm\right)\)
\(OM=\sqrt[]{5^2+5^2}=5\sqrt[]{2}\left(cm\right)\)
\(MA=\sqrt[]{5^2+10^2}=5\sqrt[]{5}\left(cm\right)\)
Chu vi \(\Delta MOA:\)
\(C=OA+OB+MA=5+5\sqrt[]{2}+5\sqrt[]{5}=5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)\left(cm\right)\)
\(\Rightarrow p=\dfrac{C}{2}=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}\left(cm\right)\)
\(\Rightarrow\left\{{}\begin{matrix}p-OA=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}-5=\dfrac{5\left(\sqrt[]{2}+\sqrt[]{5}-1\right)}{2}\\p-OB=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}-5\sqrt[]{2}=\dfrac{5\left(-\sqrt[]{2}+\sqrt[]{5}+1\right)}{2}\\p-MA=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}-5\sqrt[]{5}=\dfrac{5\left(\sqrt[]{2}-\sqrt[]{5}+1\right)}{2}\end{matrix}\right.\)
\(p\left(p-MA\right)=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}.\dfrac{5\left(1+\sqrt[]{2}-\sqrt[]{5}\right)}{2}\)
\(\Leftrightarrow p\left(p-MA\right)=\dfrac{25\left[\left(1+\sqrt[]{2}\right)^2-5\right]}{4}=\dfrac{25.2\left(\sqrt[]{2}-1\right)}{4}=\dfrac{25\left(\sqrt[]{2}-1\right)}{2}\)
\(\left(p-OA\right)\left(p-OB\right)=\dfrac{25\left[5-\left(\sqrt[]{2}-1\right)^2\right]}{4}\)
\(\Leftrightarrow\left(p-OA\right)\left(p-OB\right)=\dfrac{25.2\left(\sqrt[]{2}+1\right)}{4}=\dfrac{25\left(\sqrt[]{2}+1\right)}{4}\)
Diện tích \(\Delta MOA:\)
\(S=\sqrt[]{p\left(p-OA\right)\left(p-OB\right)\left(p-MA\right)}\)
\(\Leftrightarrow S=\sqrt[]{\dfrac{25\left(\sqrt[]{2}-1\right)}{2}.\dfrac{25\left(\sqrt[]{2}+1\right)}{2}}\)
\(\Leftrightarrow S=\sqrt[]{\dfrac{25^2}{2^2}}=\dfrac{25}{2}=12,5\left(cm^2\right)\)
Đúng 0
Bình luận (0)
| x | 0 | -5/2 | 1 |
| y=-2x-5 | -5 | 0 | |
| y=-x | 0 | -1 |
*) Đồ thị:
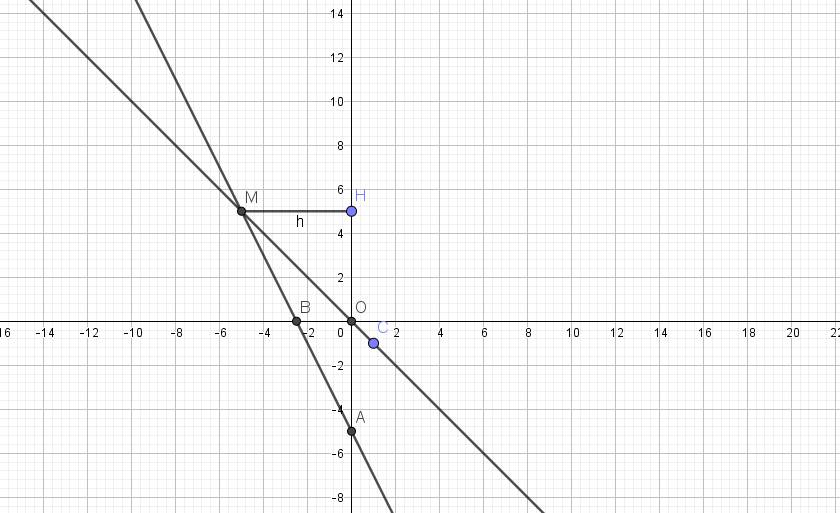
b) Phương trình hoành độ giao điểm của (d) và (d'):
\(-2x-5=-x\)
\(\Leftrightarrow-2x+x=5\)
\(\Leftrightarrow x=-5\) \(\Rightarrow y=-\left(-5\right)=5\)
Vậy tọa độ giao điểm của (d) và (d') là \(M\left(-5;5\right)\)
c) Ta có:
\(tanB=\dfrac{OA}{OB}=\dfrac{-5}{-\dfrac{5}{2}}=2\)
\(\Rightarrow\widehat{B}\simeq63^0\)
Mà góc tạo bởi d với trục hoành là \(\widehat{OBM}\)
\(\Rightarrow\widehat{OBM}\simeq180^0-63^0=117^0\)
d) Ta có:
\(OM^2=5^2+5^2=50\)
\(\Rightarrow OM=5\sqrt{2}\left(cm\right)\)
\(AM^2=5^2+10^2=125\)
\(\Rightarrow AM=5\sqrt{5}\left(cm\right)\)
Chu vi \(\Delta MOA\):
\(5\sqrt{2}+5\sqrt{5}+5=5\left(\sqrt{2}+\sqrt{5}+1\right)\left(cm\right)\)
Diện tích \(\Delta MOA\)
\(S_{MOA}=\dfrac{MH.OA}{2}=\dfrac{5.5}{2}=25\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho 2 hàm số : y 2x+4 có đồ thị là đường thẳng (d) và y -x+1 có đồ thị là đường thẳng ( d1)a, vẽ đồ thị của hai hàm số trên cùng mặt phẳng tọa độ Oxyb. gọi giao của đường thẳng (d) và (d1) với nhau là C ; giao của các đường thẳng (d) với (d1) với trục Ox là A và B . Tìm tọa độ các điểm A , B , C bằng phép tính . Tính diện tích của tam giác ABC .c, Tính góc tạo bởi đường thẳng y 2x+4 với trục Ox ( làm tròn đến độ )
Đọc tiếp
Cho 2 hàm số : y = 2x+4 có đồ thị là đường thẳng (d) và y = -x+1 có đồ thị là đường thẳng ( d1)
a, vẽ đồ thị của hai hàm số trên cùng mặt phẳng tọa độ Oxy
b. gọi giao của đường thẳng (d) và (d1) với nhau là C ; giao của các đường thẳng (d) với (d1) với trục Ox là A và B . Tìm tọa độ các điểm A , B , C bằng phép tính . Tính diện tích của tam giác ABC .
c, Tính góc tạo bởi đường thẳng y = 2x+4 với trục Ox ( làm tròn đến độ )
jdhjdhshfsjsxhxhxx udjdghxhjxhg
sao dạo này toàn người cho toán lớp 9 nhỉ khó qué
Cho hàm số y = -2x + 3
a) Vẽ đồ thị của hàm số
b) Tính góc tạo bởi đường thẳng y = -2x + 3 và trục Ox (làm tròn đến phút)
a) Vẽ đồ thị hàm số:
- Cho x = 0 thì y = 3 ta được A(0; 3)
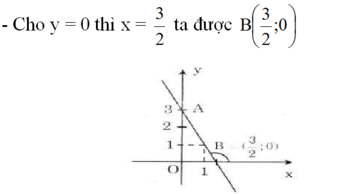
b) Gọi góc hợp bởi đường thẳng y = -2x + 3 và trục Ox là α.

Đúng 0
Bình luận (0)