Cho hàm số f(x) có f(2)=f(-2)=0 và có bảng xét dấu của đạo hàm như sau:
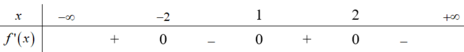
Hàm số y = f 3 - x 2 nghịch biến trên khoảng nào dưới đây?
A. (2;5)
B. (1; + ∞ )
C. (-2;-1)
D. (1;2)
Cho hàm số f(x) có f ( 2 ) = f ( - 2 ) = 0 và có bảng xét dấu của đạo hàm như sau:

Hàm số y = ( f ( 3 - x ) ) 2 nghịch biến trên khoảng nào dưới đây?
A. (2;5).
B. (1;+∞).
C. (-2;-1).
D. (1;2).
Cho hàm số y=f(x) có bảng xét dấu của đạo hàm như sau

Biết rằng f(0)+f(3)=f(2)+f(5) Giá trị nhỏ nhất, giá trị lớn nhất của hàm số f(x) trên đoạn [0;5] lần lượt là
A. f(0), f(5)
B. f(2), f(0)
C. f(1), f(5)
D. f(2), f(5)
Dựa vào bảng xét dấu của f '(x) ta có bảng biến thiên của hàm số trên đoạn [0;5] như sau
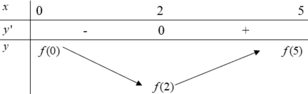
Suy ra ![]() Và
Và ![]()
Ta có ![]()
![]()
Vì f(x) đồng biến trên đoạn [2;5] nên ![]()
⇒ f(5)>f(0)
Vậy
![]()
Chọn đáp án D.
Cho hàm số y = f(x) có đạo hàm trên R và bảng xét dấu của đạo hàm như sau:
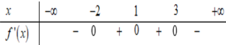
Hàm số y= f(x) có bao nhiêu điểm cực trị?
A. 2
B. 0
C. 1
D. 3
Đáp án A
Dựa vào bảng biến thiên ta thấy rằng ![]() .
.
![]() đổi dấu khi qua hai điểm
đổi dấu khi qua hai điểm ![]() và
và ![]() không đổi dấu khi qua điểm x=1 nên hàm số y= f(x) có hai diểm cực trị.
không đổi dấu khi qua điểm x=1 nên hàm số y= f(x) có hai diểm cực trị.
Cho hàm số y=f(x) có đạo hàm trên ℝ và bảng xét dấu của đạo hàm như sau:

Hàm số y=f(x)có bao nhiêu điểm cực trị?
A. 2.
B. 0.
C. 1.
D. 3.
Dựa vào bảng biến thiên ta thấy rằng f’(-2)=f’(1)=f’(3)=0.
f’(x)đổi dấu khi qua hai điểm x=-2; x=3 và f’(x) không đổi dấu khi qua điểm x=1 nên hàm số y=f(x) có hai diểm cực trị.
Đáp án A
Cho hàm số y=f(x) xác định trên R và có bảng xét dấu đạo hàm như sau:
| x | -∞ -1 1 4 +∞ |
| f'(x) | - 0 + 0 - 0 + |
Biết f(x)>2 ∀xϵR Xét hàm số \(g\left(x\right)=f\left(3-2f\left(x\right)\right)-x^3+3x^2-2020\) đồng biến, nghịch biến trên các khoảng nào?
Bài này chỉ có thể trắc nghiệm (dựa vào kết quả trắc nghiệm để suy luận) chứ không thể giải tự luận
Vì với mỗi hàm \(f\left(x\right)\) khác nhau sẽ cho những khoảng đồng biến - nghịch biến của \(g\left(x\right)\) khác nhau
Cho hàm số y = f x có đạo hàm cấp hai trên R. Biết f ' 0 = 3 ; f ' 2 = - 2018 và bảng xét dấu của f ' ' 0 như sau:
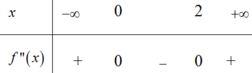
Hàm số y = f x + 2017 + 2018 x đạt giá trị nhỏ nhất tại điểm x 0 thuộc khoảng nào sau đây?
A. 0 ; 2
B. - ∞ ; - 2017
C. - 2017 ; 0
D. 2017 ; + ∞
Ta có:
![]()
Từ BXD của f ' ' x ta suy ra BBT của f ' x như sau:
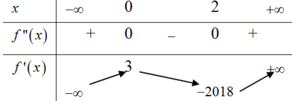
Từ BBT ta có:
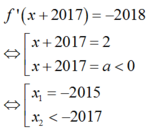
Từ đó ta suy ra BBT của hàm số f ' x + 2017 + 2018 như sau:
Tịnh tiến đồ thị hàm số y = f ' x lên trên 2018 đơn vị.
Tịnh tiến đồ thị hàm số y = f ' x sang trái 2017 đơn vị.
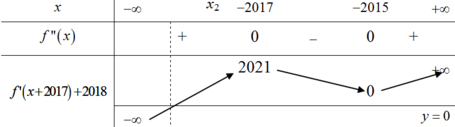
Suy ra BBT của hàm số y = f ' x + 2017 + 2018 x

Vậy hàm số đạt GTNN tại x 2 < - 2017
Chọn B.
Cho hàm số y=f(x) có bảng xét dấu của đạo hàm như sau.
x -∞ -2 -1 2 4 +∞
f’(x) + 0 - 0 + 0 - 0 +
Hàm số y =-2f(x)+2019 nghịch biến trên khoảng nào trong các khoảng dưới đây?
A. (-4 ;2)
B. (-1 ;2)
C. (-2 ;-1)
D. (2 ;4)
y’= -2f’(x) nên hàm số nghịch biến trên (-∞;-2),(-1;2) và (4;+∞).
Chọn đáp án B.
Cho hàm số y = f(x) liên tục trên R và có bảng xét dấu của đạo hàm như sau

Có bao nhiêu giá trị nguyên của tham số m để hàm số g (x) = f (x + m) đồng biến trên khoảng (0; 2).
A. 3
B. 4
C. 2
D. 1
Cho hàm số y = f(x) liên tục trên R và có bảng xét dấu của đạo hàm như sau

Có bao nhiêu giá trị nguyên của tham số m để hàm số g (x) = f (x + m) đồng biến trên khoảng (0; 2).
A. 3
B. 4
C. 2
D. 1