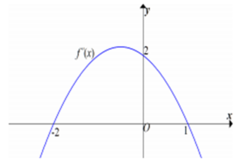
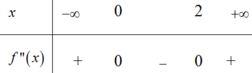Ta có:
Từ BXD của f ' ' x ta suy ra BBT của f ' x như sau:
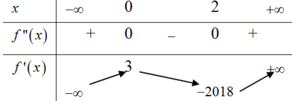
Từ BBT ta có:
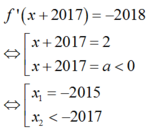
Từ đó ta suy ra BBT của hàm số f ' x + 2017 + 2018 như sau:
Tịnh tiến đồ thị hàm số y = f ' x lên trên 2018 đơn vị.
Tịnh tiến đồ thị hàm số y = f ' x sang trái 2017 đơn vị.
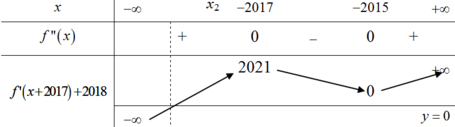
Suy ra BBT của hàm số y = f ' x + 2017 + 2018 x
Vậy hàm số đạt GTNN tại x 2 < - 2017
Chọn B.
Cho hàm số y=f(x) có bảng xét dấu của đạo hàm như sau
Biết rằng f(0)+f(3)=f(2)+f(5) Giá trị nhỏ nhất, giá trị lớn nhất của hàm số f(x) trên đoạn [0;5] lần lượt là
A. f(0), f(5)
B. f(2), f(0)
C. f(1), f(5)
D. f(2), f(5)
Cho hàm số f(x) có f ( 2 ) = f ( - 2 ) = 0 và có bảng xét dấu của đạo hàm như sau:
Hàm số y = ( f ( 3 - x ) ) 2 nghịch biến trên khoảng nào dưới đây?
A. (2;5).
B. (1;+∞).
C. (-2;-1).
D. (1;2).
Cho hàm số y=f(x) có bảng xét dấu của đạo hàm như sau.
x -∞ -2 -1 2 4 +∞
f’(x) + 0 - 0 + 0 - 0 +
Hàm số y =-2f(x)+2019 nghịch biến trên khoảng nào trong các khoảng dưới đây?
A. (-4 ;2)
B. (-1 ;2)
C. (-2 ;-1)
D. (2 ;4)
Cho hàm số liên tục trên khoảng (a;b) và x 0 ∈ a ; b . Có bao nhiêu mệnh đề đúng trong các mệnh đề sau ?
(1) Hàm số đạt cực trị tại điểm x 0 khi và chỉ khi f ' x 0 = 0
(2) Nếu hàm số y = f(x) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' x 0 = f " x 0 = 0 thì điểm x 0 không là điểm cực trị của hàm số y = f x
(3) Nếu f'(x) đổi dấu khi x qua điểm x 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f(x)
(4) Nếu hàm số y = f(x) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' x 0 = 0 , f " x 0 > 0 thì điểm x 0 là điểm cực đại của hàm số y = f(x)
A. 1
B. 2
C. 0
D. 3
Cho hàm số y = f(x) liên tục trên R và có bảng xét dấu của đạo hàm như sau
Có bao nhiêu giá trị nguyên của tham số m để hàm số g (x) = f (x + m) đồng biến trên khoảng (0; 2).
A. 3
B. 4
C. 2
D. 1
Cho hàm số y = f(x) liên tục trên R và có bảng xét dấu của đạo hàm như sau
Có bao nhiêu giá trị nguyên của tham số m để hàm số g (x) = f (x + m) đồng biến trên khoảng (0; 2).
A. 3
B. 4
C. 2
D. 1
Cho hàm số y=f(x) có đạo hàm cấp hai liên tục trên ℝ . Biết f ' − 2 = − 8 , f ' 1 = 4 và đồ thị của hàm số f"(x) như hình vẽ dưới đây. Hàm số y = 2 f x − 3 + 16 x + 1 đạt giá trị lớn nhất tại x 0 thuộc khoảng nào sau đây?
A. 0 ; 4
B. 4 ; + ∞
C. − ∞ ; 1
D. − 2 ; 1
Cho hàm số y=f(x) liên tục trên R có đạo hàm cấp 3 với f’’’(x)=0 và thỏa mãn f ( x ) ' 2018 1 - f ' ' ( x ) = 2 x ( x + 1 ) 2 ( x - 2018 ) 2019 : f ' ' ( x ) , ∀ x ∈ R Hàm số g ( x ) = f ' ( x ) 2019 1 - f ' ' ( x ) có bao nhiêu điểm cực trị?
A. 1
B.2
C.3
D. 4
Cho hàm số y = f (x) có đạo hàm trên R. Xét tính đúng sai của các mệnh đề sau.
(I): Nếu f’(x) > 0 trên khoảng (x0–h;x0) và f’(x) < 0 trên khoảng (x0;x0+h) (h>0) thì hàm số đạt cực đại tại điểm x0
(II): Nếu hàm số đạt cực đại tại điểm x0 thì tồn tại các khoảng (x0–h;x0), (x0;x0+h) (h>0) sao cho f’(x) > 0 trên khoảng (x0–h;x0) và f’(x) < 0 trên khoảng (x0;x0+h)
A. Cả (I) và (II) cùng sai
B. Mệnh đề (I) đúng, mệnh đề (II) sai
C. Mệnh đề (I) sai, mệnh đề (II) đúng
D. Cả (I) và (II) cùng đúng
