Họ nguyên hàm của hàm số f(x)=sinx+1 là
A. cosx + x + C
B. sin 2 x 2 + x + C
C. -cosx + x + C
D. cosx + C
Những câu hỏi liên quan
Nguyên hàm của hàm số
f
(
x
)
sin
x
.
2
−
cos
x
là A.
F
(
x
)
2
3
(
2
−
cos
x
)
2
−
cos
x
+
C
B.
F
(
x...
Đọc tiếp
Nguyên hàm của hàm số f ( x ) = sin x . 2 − cos x là
A. F ( x ) = 2 3 ( 2 − cos x ) 2 − cos x + C
B. F ( x ) = − 3 2 ( 2 − cos x ) 2 − cos x + C
C. F ( x ) = − 1 2 2 − cos x + C
D. F ( x ) = 2 3 2 − cos x + C
Tìm nguyên hàm của hàm số
f
(
x
)
(
sin
x
+
c
o
s
x
)
2
A.
∫
f
(
x
)
d
x
x
+
1
2
c
o
s...
Đọc tiếp
Tìm nguyên hàm của hàm số f ( x ) = ( sin x + c o s x ) 2
A. ∫ f ( x ) d x = x + 1 2 c o s 2 x + C
B. ∫ f ( x ) d x = 1 2 c o s 2 x + C
C. ∫ f ( x ) d x = - 1 2 c o s 2 x + C
D. ∫ f ( x ) d x = x - 1 2 c o s 2 x + C
Họ các nguyên hàm của hàm số f(x)
(
sin
x
+
cos
x
)
2
là
Đọc tiếp
Họ các nguyên hàm của hàm số f(x)= ( sin x + cos x ) 2 là
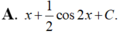
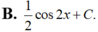
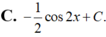
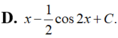
Biết F(x) là một nguyên hàm của hàm số f(x) = sin 2x + cosx. Giá trị F π 2 - F ( 0 ) bằng
A. 2.
B. 1.
C. -1.
D. 4.
Họ các nguyên hàm của hàm số
f
(
x
)
x
2
+
cos
x
là
Đọc tiếp
Họ các nguyên hàm của hàm số f ( x ) = x 2 + cos x là
Họ các nguyên hàm của hàm số
f
(
x
)
x
2
+
c
o
s
x
là A. 2x-sinx+C. B.
3
x
3
+sinx+C. C.
x
3
3
-sinx+C. D.
x
3
3
+sinx+C.
Đọc tiếp
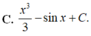
Họ các nguyên hàm của hàm số f ( x ) = x 2 + c o s x là
A. 2x-sinx+C.
B. 3 x 3 +sinx+C.
C. x 3 3 -sinx+C.
D. x 3 3 +sinx+C.
Họ nguyên hàm của hàm số
f
(
x
)
e
x
+
cos
x
+
2018
là
Đọc tiếp
Họ nguyên hàm của hàm số f ( x ) = e x + cos x + 2018 là
Họ nguyên hàm của hàm số
f
(
x
)
e
x
+
cos
x
+
2019
là
Đọc tiếp
Họ nguyên hàm của hàm số f ( x ) = e x + cos x + 2019 là
Tìm họ nguyên hàm của hàm số :
\(f\left(x\right)=\frac{5\sin x}{2\sin x-\cos x+1}\)
Biến đổi :
\(5\sin x=a\left(2\sin x-\cos x+1\right)+b\left(2\cos x+\sin x\right)+c\)
= \(\left(2a+b\right)\sin x+\left(2b-a\right)\cos x+a+c\)
Đồng nhất hệ số hai tử số :
\(\begin{cases}2a+b=5\\2b-a=0\\a+c=0\end{cases}\)
\(\Rightarrow\) \(\begin{cases}a=2\\b=1\\c=-2\end{cases}\)
Khi đó :
\(f\left(x\right)=\frac{2\left(2\sin x-\cos x+1\right)+\left(2\cos x+\sin x\right)-2}{2\sin x-\cos x+1}\)
= \(2+\frac{2\cos x+\sin x}{2\sin x-\cos x+1}-\frac{2}{2\sin x-\cos x+1}\)
Do vậy :
\(I=2\int dx+\int\frac{\left(2\cos x+\sin x\right)dx}{2\sin x-\cos x+1}-2\int\frac{dx}{2\sin x-\cos x+1}\)
=\(2x+\ln\left|2\sin x-\cos x+1\right|-2J+C\)
Với
\(J=\int\frac{dx}{2\sin x-\cos x+1}\)
Đúng 0
Bình luận (0)