Tìm các giá trị a , b ∈ ℝ để hệ phương trình x y - 1 x y + 1 = a x 2 + y 2 = b (x>0) có nghiệm duy nhất.
A. a=0;b=1
B. a=1,b=2
C. a=0; 0 < b ≤ 1
D. a=0;b=2
Tìm tất cả các giá trị thực của tham số m để bất phương trình ![]() nghiêm đúng với mọi giá trị x (1;64)
nghiêm đúng với mọi giá trị x (1;64)
A. m ≤ 0
B. m ≥ 0
C. m < 0
D. m > 0
Đáp án B.
![]()
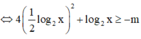
Đặt ![]()
Khi đó bài toán trở thành ![]()
Lập bảng biến thiên suy ra 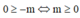
Tìm tất cả các giá trị thực của tham số m để bất phương trình 4 log 2 x x + log 2 x + m ≥ 0 nghiêm đúng với mọi giá trị x ∈ 1 ; 64 .
![]()
![]()
![]()
![]()
Cho hàm số y = - x 4 + 2 x 2 có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình - x 4 + 2 x 2 = log 2 m có bốn nghiệm thực phân biệt.
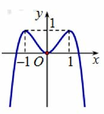
A. 1 < m < 2 .
B. 0 ≤ m ≤ 1 .
C. m ≥ 2 .
D. m > 0 .
Tìm các giá trị a ∈ ℝ để phương trình log 3 3 - x = a có nghiệm.
A. a ≥ 0
B. b ≤ a ≤ 1
C. a ≤ 1
D. ∀ a ∈ ℝ
Cho phương trình m - 4 x 2 - 2 m - 2 x + m - 1 = 0 (m là tham số). Tập hợp tất cả các giá trị của m để phương trình có hai nghiệm trái dấu và nghiệm âm có giá trị tuyệt đối lớn hơn nghiệm dương là
A. 2 ; 4
B. 2 ; 4
C. 1 ; 2
D. ∅
Cho phương trình x2 +( m-1)x - m = 0 (5)
a/ Chứng tỏ rằng phương trình (5) luôn có nghiệm với mọi giá trị của m ?
b/ Gọi x1 và x2 là nghiệm của phương trình (5) Chứng minh hệ thức
x1^2 +x2^2 -2.x1.x2 -x1^2.x2^2 =2m+1
a: \(\text{Δ}=\left(m-1\right)^2-4\cdot1\cdot\left(-m\right)=\left(m+1\right)^2>=0\)
=>(5) luôn có nghiệm
b: \(x_1^2+x_2^2-2x_1x_2-\left(x_1\cdot x_2\right)^2=2m+1\)
=>\(\left(x_1+x_2\right)^2-4x_1x_2-\left(x_1\cdot x_2\right)^2=2m+1\)
=>\(\left(m-1\right)^2-4\cdot\left(-m\right)-\left(-m\right)^2=2m+1\)
=>\(m^2-2m+1+4m-m^2=2m+1\)
=>2m+1=2m+1(luôn đúng)
Cho hàm số y = f x liên tục trên ℝ sao cho m a x - 1 ; 2 f x = 3 . Xét g x = f 3 x - 1 + m . Tìm tất cả các giá trị của tham số m để m a x 0 ; 1 g x = - 10 .
![]()
![]()
![]()
![]()
Tìm các giá trị m ∈ ℝ để bất phương trình 2 sin 2 x + 3 cos 2 x ≤ m . 3 sin 2 x nghiệm đúng .
A. m ≥ 4
B. m ≤ 6
C. m ≤ 1
D. m ≥ 1
Cho hệ phương trình: a2x + y = 1 và x + y = a
a, giải hệ phương trình với a = -2
b, tìm các giá trị của a để hệ phương trình có vô số nghiệm
c, tìm a để hệ phương trình có nghiệm duy nhất (x,y) thỏa mãn x,y đều nguyên