Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, A B = a 3 , B C = a 2 . Cạnh bên S A = a và SA vuông góc với mặt phẳng đáy. Khoảng cách giữa SB và DC bằng:
A. a 2
B. 2 a 3
C. a 3
D. a 3 2
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật cạnh a, S A ⊥ (A B C D) ,SC tạo với mặt đáy một góc 60 độ và (SAB ) một góc a với sin a = căn 3/ 4 . Tính chiều cao khối chóp.
Đáy là hình vuông hay chữ nhật bạn? Hình chữ nhật sao có các cạnh bằng nhau và bằng a được?
Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a, AD = a 2 , SA⊥(ABCD) góc giữa SC và đáy bằng 60°. Thể tích hình chóp S.ABCD bằng:
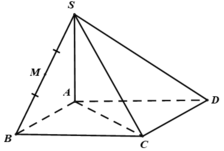
A. a 3 2
B. 3 a 3 2
C. 3 a 3
D. a 3 6
Đáp án A
Theo bài ra ta có:
SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
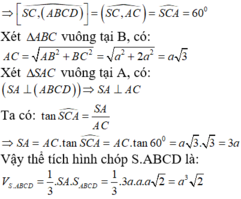
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt đáy (ABCD), AB = a, AD = 2a, SA =a. Tính thể tích khối chóp S.ABCD.
A. 2a3
B. a3
C. a3/3
D. 2a3/3
Đáp án D
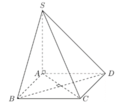
Diện tích hình chữ nhật ABCD là S = 2a2, chiều cao SA =a.
Vậy thể tích khối chóp S.ABCD là V = 1 3 . 2 a 2 . a = 2 3 a 3
1.Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB= \(\dfrac{a\sqrt{3}}{3}\), AD=a\(\sqrt{3}\), SA=a và vuông góc với mp đáy. Khi đó góc giữa SB và mp (SAD) bằng bao nhiêu?
2.Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B. SA vuông góc với mp đáy. Số mặt của tứ diện là tam giác vuông là bao nhiêu?
3. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, CA=a, CB=b, SA=h vuông góc với mặt đáy. Gọi I là trung điểm của AB.
a, CMR: BC vuông góc với (SAC)
b, Tính khoảng cách giữa SI và AC theo a,b,h
3.
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\BC\perp AC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAC\right)\)
b.
Gọi M là trung điểm BC \(\Rightarrow IM||AC\)
\(\Rightarrow AC||\left(SIM\right)\Rightarrow d\left(AC;SI\right)=d\left(AC;\left(SIM\right)\right)=d\left(A;\left(SIM\right)\right)\)
Qua A kẻ đường thẳng song song BC cắt IM kéo dài tại K
\(\Rightarrow IM\perp AK\Rightarrow IM\perp\left(SAK\right)\)
Trong mp (SAK), kẻ AH vuông góc SK
\(\Rightarrow AH\perp\left(SIM\right)\Rightarrow AH=d\left(A;\left(SIM\right)\right)\)
\(AK=CM=\dfrac{b}{2}\)
\(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AK^2}\Rightarrow AH=\dfrac{SA.AK}{\sqrt{SA^2+AK^2}}=\dfrac{\dfrac{h.b}{2}}{\sqrt{h^2+\dfrac{b^2}{4}}}=\dfrac{bh}{\sqrt{b^2+4h^2}}\)
1.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AB\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAD\right)\)
\(\Rightarrow\widehat{SBA}\) là góc giữa SB và (SAD)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=\sqrt{3}\Rightarrow\widehat{SBA}=60^0\)
2.
\(SA\perp\left(ABC\right)\Rightarrow\left\{{}\begin{matrix}SA\perp AB\\SA\perp AC\end{matrix}\right.\) \(\Rightarrow\) các tam giác SAB và SAC vuông
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\)
\(\Rightarrow\) Tam giác SBC vuông
Vậy tứ diện có 4 mặt đều là tam giác vuông (ABC hiển nhiên vuông theo giả thiết)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. AB=a, BC=2a cạnh bên SA vuông góc với đáy và SA=a 2 Tính thể tích khối chóp S.ABCD
A. 2 3 a 3 3
B. 2 2 a 3 3
C. 2 2 a 3
D. 2 a 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt đáy (ABCD), AB = a, AD = 2. Góc giữa cạnh bên SB và mặt phẳng (ABCD) bằng 45°. Thể tích hình chóp S.ABCD bằng
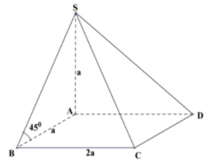
A. 6 a 3 18
B. 2 2 a 3 3
C. a 3 3
D. 2 a 3 3
Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a, AD = a 2 ; SA ⊥ (ABCD), góc giữa SC và đáy bằng 60°. Thể tích hình chóp S.ABCD bằng:
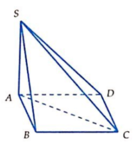
A. a 3 2
B. 3 a 3
C. a 3 6
D. 3 a 3 2
Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a, AD = a 2 , SA⊥(ABCD) góc giữa SC và đáy bằng 60°. Thể tích hình chóp S.ABCD bằng:
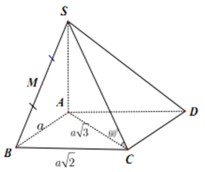
A. a 3 2
B. a 3 6
C. 3 a 3
D. 3 a 3 2
Đáp án A
SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
Xét ΔABC vuông tại B, có

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=a,AD=2a Biết SA vuông góc với mặt phẳng đáy và SA=3a . Thể tích hình chóp S.ABCD là:
A. 6 a 3
B. 2 a 2
C. 2 a 3
D. a 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a. Biết SA vuông góc với mặt phẳng đáy và SA = 3a. Thể tích hình chóp S.ABCD là:
A. 6 a 3
B. 12 a 3
C. 2 a 3
D. 1 3 a 3