Tìm tập giá trị G của hàm số y = log 4 x - x 2 .
A. G = 0 ; 1
B. G = [ - 1 ; 0 )
C. G = - ∞ ; - 1
D. G = ℝ
Cho đồ thị của hàm số \(y = {\log _2}x\) và y = 2 như Hình 6.8. Tìm khoảng giá trị của x mà đồ thị hàm số \(y = {\log _2}x\) nằm phía trên đường thẳng y = 2 và từ đó suy ra tập nghiệm của bất phương trình \({\log _2}x > 2.\)

Khoảng giá trị của x mà đồ thị hàm số \(y=log_2x\) nằm phía trên đường thẳng y = 2 là \(\left(4;+\infty\right)\)
\(\Rightarrow\) Tập nghiệm của bất phương trình \(log_2x>2\) là \(\left(4;+\infty\right)\)
Tìm tất cả các giá trị thực của tham số m để hàm số y = log ( x 2 - 2 m x + 4 ) có tập xác định là ℝ .
A . - 2 ≤ m ≤ 2
B . m = 2
C . m > 2 h o ặ c m < - 2
D . - 2 < m < 2
Chọn D
y = log ( x 2 - 2 m x + 4 )
Điều kiện xác định của hàm số trên ![]()
Để tập xác định của hàm số là
ℝ
thì 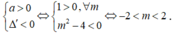
Vậy đáp án đúng là đáp án D.
Tìm tất cả các giá trị thực của tham số m để hàm số y = log ( x 2 - 2 m x + 4 ) có tập xác định là R
A. - 2 ≤ m ≤ 2
B. m = 2
![]()
D. -2 < m < 2
Cho hàm số lôgarit \(y = {\log _2}x\)
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau: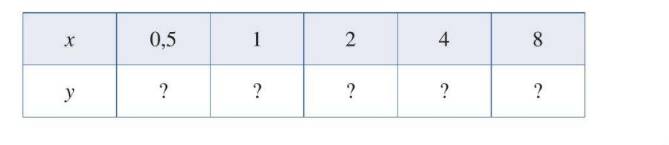
b, Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a.
Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;{{\log }_2}x} \right)\) với \(x \in (0; + \infty )\) và nối lại ta được đồ thị hàm số \(y = {\log _2}x\) như hình bên.
c, Cho biết tọa độ giao điểm của đồ thị hàm số \(y = {\log _2}x\) với trục hoành và vị trí của đồ thị hàm số đó với trục tung.
d, Quan sát đồ thị hàm số \(y = {\log _2}x\), nêu nhận xét về:
\(\mathop {\mathop {\lim }\limits_{x \to {0^ + }} ({{\log }_2}x)}\limits_{} \,;\mathop {\,\,\mathop {\lim }\limits_{x \to + \infty } ({{\log }_2}x)}\limits_{} \)Sự biến thiên của hàm số \(y = {\log _2}x\) và lập bảng biến thiên của hàm số đóa:
| x | 0,5 | 1 | 2 | 4 | 8 |
| \(y\) | -1 | 0 | 1 | 2 | 3 |
b:
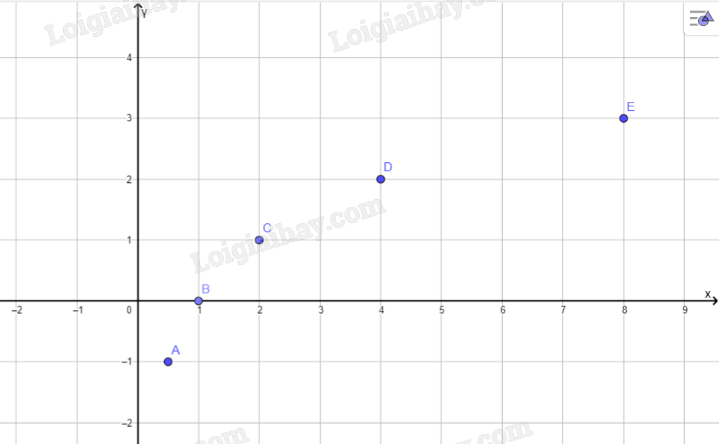
c: Tọa độ giao điểm của hàm số với trục hoành là B(2;0)
Đồ thị hàm số này ko cắt trục tung
d:
\(\lim\limits_{x\rightarrow0^+}log_2x=0\)
\(\lim\limits_{x\rightarrow+\infty}\left(log_2x\right)=+\infty\)
=>Hàm số này đồng biến trên TXĐ của nó là D=[0;+vô cực)

Tìm tập xác định của các hàm số sau:
a) \(y = \log \left| {x + 3} \right|;\)
b) \(y = \ln \left( {4 - {x^2}} \right).\)
a, \(y=log\left|x+3\right|\) có nghĩa khi \(\left|x+3\right|>0\)
Mà \(\left|x+3\right|\ge0\forall x\in R\)
\(\Rightarrow\) \(\left|x+3\right|>0\) khi \(x\ne-3\)
Vậy tập xác định của hàm số là D = R \ {-3}.
b, \(y=ln\left(4-x^2\right)\) có nghĩa khi \(4-x^2>0\)
\(\Rightarrow x^2< 4\\ \Leftrightarrow-2< x< 2\)
Vậy tập xác định của hàm số là D = (-2;2).
Tìm tập xác định của các hàm số:
a) \(y = 12{}^x\)
b) \(y = {\log _5}(2x - 3)\)
c) \(y = {\log _{\frac{1}{5}}}\left( { - {x^2} + 4} \right)\)
\(a,D=R\\ b,2x-3>0\\ \Rightarrow x>\dfrac{3}{2}\\ \Rightarrow D=(\dfrac{3}{2};+\infty)\\ c,-x^2+4>0\\ \Rightarrow x^2< 4\\ \Leftrightarrow-2< x< 2\\ \Rightarrow D=\left(-2;2\right)\)
Tìm tập xác định của hàm số y = log x 2 - x - 2
A. - ∞ ; 2
B. 1 ; + ∞
C. - ∞ ; - 1 ∪ 2 ; + ∞
D. - 1 ; 1
Tìm tập xác định của hàm số y = log ( x 2 - x - 2 )
A. ( - ∞ ; - 1 ) ∪ ( 2 ; + ∞ )
B. ( - ∞ ; 2 )
C. ( 1 ; + ∞ )
D. (-1; 1)
Tìm tập xác định của hàm số y=log ( x2-x-2)
![]()
![]()
![]()
![]()
tìm tập giá trị của hàm số y = \(\dfrac{\sqrt[]{x}-2}{x-4}\)
Lời giải:
TXĐ: $[0; +\infty)\setminus\left\{4\right\}$
$y=\frac{\sqrt{x}-2}{x-4}=\frac{\sqrt{x}-2}{(\sqrt{x}-2)(\sqrt{x}+2)}=\frac{1}{\sqrt{x}+2}$
Ta có:
$\sqrt{x}\geq 0\Rightarrow y\leq \frac{1}{2}$ với mọi $x\in TXĐ$
$\sqrt{x}+2>0$ với mọi $x\in TXĐ$ nên $y>0$ với mọi $x\in TXĐ$
Vậy TGT của hàm số là $(0; \frac{1}{2}]$