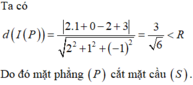Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x-2y-z-9=0 và mặt cầu (S): ( x - 3 ) 2 + ( y + 2 ) 2 + ( z - 1 ) 2 = 100 . Biết (P) cắt (S) theo giao tuyến là một đường tròn. Tâm của đường tròn giao tuyến đó có tọa độ là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x − 2 2 + y − 1 2 + z 2 = 1 và mặt phẳng Q : 2 x − 2 y − z + 1 = 0 . Viết phương trình mặt cầu (S') đối xứng với mặt cầu (S) qua mặt phẳng (Q)
A. x + 2 3 2 + y − 7 3 2 + z − 2 3 2 = 1
B. x − 2 3 2 + y − 7 3 2 + z + 2 3 2 = 1
C. x − 2 3 2 + y + 7 3 2 + z − 2 3 2 = 1
D. x − 2 3 2 + y − 7 3 2 + z − 2 3 2 = 1
Đáp án D
Mặt cầu S 1 có tâm M(2;1;0) và có bán kính R 1 = 1
Gọi M' là hình chiếu vuông góc của M trên mặt phẳng (Q)
Ta có M M ' ⊥ Q nên đường thẳng MM' đi qua điểm M và nhận vectơ pháp tuyến của mặt phẳng (Q) làm vectơ chỉ phương.
=> phương trình tham số đường thẳng MM': x = 2 + 2 t y = 1 − 2 t z = − t , t ∈ ℝ
Vì M' là hình chiếu vuông góc của M trên mặt phẳng Q ⇒ M ' = M M ' ∩ Q
=> tọa độ điểm M' là nghiệm hệ phương trình:
2 x − 2 y − z + 1 = 0 x = 2 + 2 t y = 1 − 2 t z = − t ⇔ 2 2 + t − 2 1 − 2 t − − t + 1 = 0 x = 2 + 2 t y = 1 − 2 t z = − t ⇔ t = − 1 3 x = 4 3 y = 5 3 z = 1 3
⇒ M ' 4 3 ; 5 3 ; 1 3
Gọi I(x;y;z) là tâm của mặt cầu (S'), do mặt cầu (S') đối xứng với mặt cầu (S) qua mặt phẳng (Q) => I đối xứng với M qua mặt phẳng (Q)
=> I đối xứng với M qua mặt phẳng M'
=> M' là trung điểm của đường thẳng IM.
⇒ x = 2 x M ' − x M = 2 3 y = 2 y M ' − y M = 7 3 z = 2 z M ' − z M = 2 3 ⇒ I 2 3 ; 7 3 ; 2 3
Khi đó mặt cầu (S') có tâm I 2 3 ; 7 3 ; 2 3 , bán kính R' = R = 1 nên có phương trình:
x − 2 3 2 + y − 7 3 2 + z − 2 3 2 = 1
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 2 ) 2 = 9 và mặt phẳng (P): 2x - 2y + z + 3 = 0. Gọi M(a;b;c) là điểm trên mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) là lớn nhất. Khi đó:
A. a + b + c = 8.
B. a + b + c = 5.
C. a + b + c = 6.
D. a + b + c = 7.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng ( P ) : 2 x − 2 y − z − 9 = 0 và mặt cầu ( S ) : ( x − 3 ) 2 + ( y + 2 ) 2 + ( z − 1 ) 2 = 100 . Biết (P) cắt (S) theo giao tuyến là một đường tròn. Tìm tọa độ tâm của đường tròn giao tuyến.
A. (3;2;-1)
B. (-3;2;-1)
C. (3;-2;1)
D. (-3;2;1)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : 2 x - 2 y - z - 9 = 0 và mặt cầu S : x - 3 2 + y + 2 2 + z - 1 2 = 100 . Biết (P) cắt (S) theo giao tuyến là một đường tròn. Tâm của đường tròn giao tuyến đó có tọa độ là
A. (3;2;-1)
B. (-3;2;-1)
C. (3;-2;1)
D. (-3;2;1)
Chọn C.
Phương pháp: Tâm đường tròn giao tuyến của mặt phẳng và mặt cầu là giao điểm của mặt phẳng đó và đường thẳng đi qua tâm mặt cầu vuông góc với mặt phẳng.
Cách giải: Phương trình đường thẳng d đi qua tâm mặt cầu (S) và vuông góc với mặt phẳng (P) là:
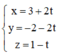
Tọa độ tâm đường tròn giao tuyến thỏa mãn hệ
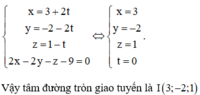
Chú ý: Bài toán cho vào trường hợp đặc biệt là tâm mặt cầu nằm trên mặt phẳng.
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): \(x^2+y^2+z^2-2x+6y-8z-10=0\) và mặt phẳng (P): \(x+2y-2z=0\). Viết phương trình mặt phẳng (Q) song song với (P) và tiếp xúc với (S).
Trong không gian với hệ tọa độ Oxyz, cho điểm M 2 ; 1 ; 0 và mặt phẳng Q : 2 x + 2 y − z + 1 = 0 . Viết phương trình mặt cầu (S) tâm M và tiếp xúc với mặt phẳng (Q)
A. S : x − 2 2 + y − 1 2 + z 2 = 7 3
B. S : x + 2 2 + y + 1 2 + z 2 = 7 3
C. S : x − 2 2 + y − 1 2 + z 2 = 49 9
D. S : x + 2 2 + y + 1 2 + z 2 = 49 9
Đáp án C.
Mặt phẳng (Q) có vectơ pháp tuyến n → 2 ; − 2 ; − 1
Mặt cầu (S) tâm M và tiếp xúc với mặt phẳng (Q) nên có bán kính R = d M , Q = 2.2 + 2 + 1 4 + 4 + 1 = 7 3
Phương trình mặt cầu S : x − 2 2 + y − 1 2 + z 2 = 49 9
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : 2 x + 2 y - z - 3 = 0 và điểm I(1;2; −3). Mặt cầu (S) tâm I và tiếp xúc mp (P) có phương trình:
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S): x - 1 2 + y 2 + z - 2 2 = 9 và mặt phẳng (P): 2x + y - z + 3 = 0 . Khẳng định nào sau đây là đúng?
A. Tâm của mặt cầu (S) nằm trên mặt phẳng (P)
B. Mặt phẳng (P) cắt mặt cầu (S)
C. Mặt phẳng (P) không cắt mặt cầu (S)
D. Mặt phẳng (P) tiếp xúc với mặt cầu (S)
Chọn B
Mặt cầu (S) có tâm I(1;0;2) và bán kính R = 3.
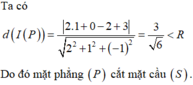
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu S : x - 1 2 + y 2 + z - 2 2 = 9 và mặt phẳng P : 2 x + y - z + 3 = 0 . Khẳng định nào sau đây là đúng?
A. Tâm của mặt cầu S nằm trên mặt phẳng P
B. Mặt phẳng P cắt mặt cầu S
C. Mặt phẳng P không cắt mặt cầu S
D. Mặt phẳng P tiếp xúc với mặt cầu S
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S): x - 1 2 + y 2 + z - 2 2 = 9 và mặt phẳng (P): 2x + y - z + 3 = 0 . Khẳng định nào sau đây là đúng?
A. Tâm của mặt cầu (S) nằm trên mặt phẳng (P)
B. Mặt phẳng (P) cắt mặt cầu (S)
C. Mặt phẳng (P) không cắt mặt cầu (S)
D. Mặt phẳng (P) tiếp xúc với mặt cầu (S)
Chọn B
Mặt cầu (S) có tâm I(1;0;2) và bán kính R = 3.