Biết n ∈ ℤ + , n > 4 và thỏa mãn A n 0 0 ! + A n 1 1 ! + A n 2 2 ! + A n 3 3 ! + . . . + A n n n ! = 32 n - 4 . Tính P = 1 n n + 1
A. P = 1 42
B. P = 1 30
C. P = 1 56
D. P = 1 72
Biết n ∈ ℤ + , n > 4 và thỏa mãn A n 0 0 ! + A n 1 1 ! + A n 2 2 ! + A n 3 3 ! + . . . + A n n n ! = 32 n - 4 Tính P = 1 n ( n + 1 )
A. 1 42
B. 1 30
C. 1 56
D. 1 72
Cho số phức z = 1 + i n , biết n ∈ ℤ và thỏa mãn log 2 8 − n + log 2 n + 3 = log 2 10
Tính môđun của số phức z
A. 8
B. z = 8 2 hoặc z = 1 2
C. 4 2
D. 2
Cho số phức z = i + 1 n , biết n ∈ ℤ và thỏa mãn log 2 8 - n + log 2 n + 3 = log 2 10 .
Tính môđun của số phức z.
A. 2
B. 4 2
C. 8
D. z = 8 2 h o ặ c z = 1 2
Cho khai triển ( 1 + 2 x ) n = a 0 + a 1 x + a 2 x 2 + . . . + a n x n , trong đó n ∈ ℤ + . Biết các hệ số a 0 , a 1 , . . . , a n thỏa mãn hệ thức a 0 + a 1 2 + . . . + a n 2 n = 4096 . Hệ số a 8 bằng
A. 130272
B. 126720
C. 130127
D. 213013
Chọn B
Ta có: ![]()
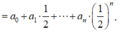
Trong khai triển ( 1 + 2 x ) n = a 0 + a 1 x + a 2 x 2 + . . . + a n x n thay x = 1 2 ta được
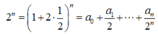
![]()
Số hạng tổng quát trong khai triển ![]()
Để có số hạng chứa x 8 thì k = 8.
Vậy ![]()
Biết n ∈ Z + , n > 4 và thỏa mãn A n 0 0 ! + A n 1 1 ! + . . . + A n n n ! = 32 n - 4 Tính P = 1 n ( n + 1 )
A. P = 1 42
B. P = 1 30
C. P = 1 56
D. P = 1 72
Biết hai số m; n thỏa mãn 7m = 4n và n - m =24. Giá trị của m; n là: |
| A. m = 7; n = 4 | B. m = 4; n = 7 | C. m = 32; n = 56 | D. m = 56; n = 32 |
B1:1 số tự nhiên A thỏa mãn A chia 25 dư \13 và A chia 4 dư 2 . Tìm 2 chữ số tận cùng của a
B2:cho n số nguyên lẻ a1,a2,...an (n>2007) thỏa mãn a1^2+...+a2005^2=a2006^2+...+an^2 tìm giá trị nhỏ nhất của n và chỉ ra 1 bộ sô a1,a1,...an thỏa mãn tìm được
a; tìm các sô nguyên dương a,b,c. Biết rằng a^3 -b^3-c^3=3.abc và a^2 = 2 (b+c)
b; tìm số tự nhiên n thỏa mãn : 2.2^2+3.2^3+4.2^4+.........+n.2^n=2^n+34
a) Tìm số tự nhiên n biết (4n+2) ⋮ (n+1)
b) Tìm các số nguyên a và b thỏa mãn: (a+2).(b-1)=9
Cíuuu tuiiii
a: =>4n+4-2 chia hết cho n+1
=>\(n+1\in\left\{1;-1;2;-2\right\}\)
mà n là số tự nhiên
nên \(n\in\left\{0;1\right\}\)
b: \(\Leftrightarrow\left(a+2;b-1\right)\in\left\{\left(1;9\right);\left(9;1\right);\left(-1;-9\right);\left(-9;-1\right);\left(3;3\right);\left(-3;-3\right)\right\}\)
=>\(\left(a,b\right)\in\left\{\left(-1;10\right);\left(7;2\right);\left(-3;-8\right);\left(-11;0\right);\left(1;4\right);\left(-5;-2\right)\right\}\)