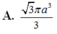
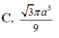
trong không gian Oxyz, cho tam giác ABC vuông cân tại C và có các đỉnh A\(\in\)(Oxz), B(-2;3;1) và C(-1;1;-1). Tìm tọa độ điểm A.
Do \(A\in\left(Oxz\right)\Rightarrow A\left(x;0;z\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{CA}=\left(x+1;-1;z+1\right)\\\overrightarrow{CB}=\left(-1;2;2\right)\end{matrix}\right.\)
Theo đề bài: \(\left\{{}\begin{matrix}\overrightarrow{CA}.\overrightarrow{CB}=0\\CA=CB\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-\left(x+1\right)-2+2\left(z+1\right)=0\\\left(x+1\right)^2+1+\left(z+1\right)^2=1+4+4\end{matrix}\right.\)
Hi vọng là bạn tự giải được hệ pt rất cơ bản này
Trong không gian, cho tam giác ABC vuông tại A, AB = a và AC = a 3 . Khi quay tam giác ABC xung quanh AB, ta được một khối nón có độ dài đường sinh là:
A. l = 2a B. l = a 2
C. l = a 3 D. l = a
Chọn A.
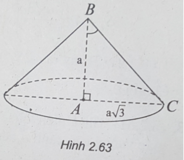
(h.2.63) Độ dài đường sinh l bằng độ dài cạnh BC của tam giác vuông ABC.
Theo định lý Py-ta-go, ta có:
BC 2 = AB 2 + AC 2 = a 2 + 3 a 2 = 4 a 2
⇒ BC = 2a.
Vậy độ dài đường sinh của hình nón là l = 2a.
Trong không gian Oxyz, cho tam giác ABC với A − 4 ; 9 ; − 9 , B 2 ; 12 ; − 2 và C − m − 2 ; 1 − m ; m + 5 . Tìm giá trị của m để tam giác ABC vuông tại B.
A. m = − 4
B. m = 4
C. m = − 3
D. m = 3
Đáp án A
Ta có:
B A → = − 6 ; − 7 ; − 3
B C → = − m − 4 ; − m − 11 ; m + 7
Mặt khác: B A → . B C → = 0 nên m = − 4 .
Câu 1. Tam giác ABC cân tại B có
0 B 40 thì A bằng:
A) 400 B) 70
0 C) 60
0 D) 50
0
Câu 2. Tam giác AED có AD2 = DE2 - AE2thì tam giác AEDA) vuông tại E B) vuông tại D C) vuông tại A D) không vuôngCâu 3. Cho tam giác ABC và tam giác có ba đỉnh D; E; F, biết AB = EF, B =F . Cần thêm điềukiện gì để hai tam giác bằng nhau theo trường hợp: góc - cạnh - góc?A) AC = FD B) A =F C) C=E D) A=ECâu 4. Cho tam giác DEF vuông cân tại D, có DE=3cm thì EF bằng:A) 18cm B) 12cm C) 12 cm D) 18 cm
II. BÀI TẬP TỰ LUẬN (8 điểm)Cho tam giác ABC có
0 A 90 và AB < BC. Gọi M là trung điểm của AC, trên tia đối của tia MB
lấy điểm D sao cho MD = MB. 1) Chứng minh ABM = CDM từ đó chứng minh AB=CD và AB //
Câu 1: B
Câu 2:Sửa đề: \(AD^2=DE^2+AE^2\)
=> Chọn A
Câu 3: Chọn D
Câu 4: \(EF=3\sqrt{2}cm\)
Trong không gian cho tam giác ABC vuông tại A có AB=a và A C B ^ = 30 ° . Thể tích khối nón sinh ra khi quay tam giác ABC quanh trục AC là:
A. 3 πa 3 3
B. 3 πa 3
C. 3 πa 3 9
D. πa 3
Trong không gian cho tam giác ABC vuông tại A có AB=a và BC=2a. Quay tam giác ABC xung quanh cạnh AB ta thu được khối nón có thể tích bằng
A. π a 3 .
B. 3 π a 3 .
C. 3 3 π a 3 .
D. 2 3 π a 3 .
Trong không gian cho tam giác ABC vuông tại A có A B = a và B C = 2 a . Quay tam giác ABC xung quanh cạnh AB ta thu được khối nón có thể tích bằng
A. πa 3
B. 3 πa 3
C. 3 3 πa 3
D. 2 3 πa 3
Trong không gian với hệ tọa độ Oxyz, cho A(2;1;-1), B(3;0;1). Tìm điểm C ∈ O z sao cho tam giác ABC vuông tại B
A. C 0 ; 3 2 ; 0 .
B. C 0 ; 0 ; 5 2 .
C. C 0 ; 0 ; 3 .
D. C 0 ; 0 ; 5 .
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(2;0;0) , B(1;-4;0), C(0;-2;6) và mặt phẳng ( α ) : x + 2y + z- 5 = 0. Gọi H(a;b;c) là hình chiếu vuông góc của trọng tâm tam giác ABC lên mặt phẳng ( α ) . Tính P = a - b + c.
A. 5
B. -3
C. 3
D. -1
