Để bất phương trình x - 6 1 - x m - 1 6 x - 2 6 x + 2 m + 1 ≥ 0 thỏa mãn với mọi x thuộc đoạn 0 ; 1
A. m ≥ 1 4
B. m ≤ 1 2
C. 1 4 ≤ m ≤ 1 2
D. m ≤ 1 3
1.Cho \(f\left(x\right)=mx^2+\left(4m-3\right)x+4m-6\). Tìm m để bất phương trình \(f\left(x\right)\ge0\) đúng với \(\forall x\in\left(-1;2\right)\)
2. Cho bất phương trình \(x^2-4x+2|x-3|-m< 0\). Tìm m để bất phương trình đã cho đúng với \(\forall x\in\left[1;4\right]\)
Cho bất phương trình x + 6 + m > x 6 − 3 . Tìm m để bất phương trình có nghiệm x = 3.
Bài 1: Cho bất phương trình \(4\sqrt{\left(x+1\right)\left(3-x\right)}\le x^2-2x+m-3\). Xác định m để bất phương trình nghiệm \(\forall x\in[-1;3]\)
Bài 2: Cho bất phương trình \(x^2-6x+\sqrt{-x^2+6x-8}+m-1\ge0\). Xác định m để bất phương trình nghiệm đúng \(\forall x\in[2;4]\)
Tìm m để các bất phương trình sau là bất phương trình bậc nhất ẩn x:
a) ( 2 m 2 − 4 ) x − m ≥ 0 b) ( 3 m − 1 ) x 3 − x + 6 < 0 ;
c) x m 2 + 3 m − 4 − 2 m ≤ 0 ; d) ( 2 m + 9 ) x + 5 5 m + 10
Cho bất phương trình 3 + x + 6 - x - 18 + 3 x - x 2 ≤ m 2 - m + 1 (m là tham số). Có bao nhiêu giá trị nguyên của m thuộc[-5;5] để bất phương trình nghiệm đúng với mọi x ∈ - 3 ; 6 ?
A. 3
B. 5
C. 9
D. 10
Đặt ![]()
Suy ra ![]()
Ta có ![]()
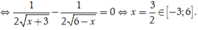
Ta có bảng biến thiên
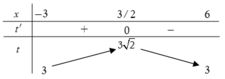
Từ bảng biến thiên ta suy ra ![]()
Khi đó bất phương trình trở thành: ![]()
![]()
Xét hàm số ![]() với
với ![]()
Ta có ![]()
Suy ra hàm số f(t) nghịch biến trên ![]()
![]()
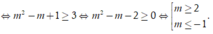
Chọn C.
Tìm a để các bất phương trình sau là bất phương trình bậc nhất ẩn x:
a) a − 5 x < 6 ; b) ( 2 a 2 − 1 ) x + 7 ≥ 0 ;
c) − a + 9 3 x − 3 a 5 < 0 ; d) ax − 5 3 − a ≤ 0 .
Cho bất phương trình x² -m(x-1) ≥ 0 . Tìm m để bất phương trình đúng với ∀x∈R
\(x^2-m\left(x-1\right)\ge0\Leftrightarrow x^2-mx+m\ge0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=1>0\\\Delta\le0\end{matrix}\right.\Leftrightarrow m^2-4m\le0\Leftrightarrow0\le m\le4\)
5A. Các cặp bất phương trình sau đây có tương đương không?
a) x≤3 và 2x≤6 b) x2 + 3 >0 và |3x+1| < -1
5B. bất phương trình sau đây có tương đương không? Vì saO
a) 2+x >4 và -x < -2 b) ( x2+1 )x ≥ 0 và 2x4 ≥ 0
6A. Cho hai bất phương trình x+5 ≥ |m2+2m| + 12 và x≥7 . Tìm m để hai bất phương trình tương đương.
6B. Tìm các giá trị của m để hai bất phương trình x< -2 và x< \(\frac{m^2+4m-9}{2}\) tương đương.
Điều kiện của m để bất phương trình (m+ 2) x > 2m2 - 6 (*) nghiệm đúng với mọi x < 1
A. m > -2
B. m = -2
C. m < -2
D. không có m
Chọn D
+ TH1: Với m> - 2 , bất phương trình (*) trở thành: 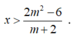
Tập nghiệm của bất phương trình là 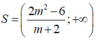
Để bất phương trình đã cho nghiệm đúng với mọi x < 1thì 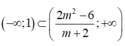
Suy ra không ra giá trị nào của m thỏa mãn.
+ TH2: m = -2, bất phương trình (*) trở thành: 0x > 2
Bất phương trình vô nghiệm
+ TH3: Với m< - 2 , bất phương trình (*) trở thành: 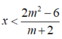
Tập nghiệm của bất phương trình là 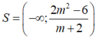
Để bất phương trình đã cho nghiệm đúng với mọi x< 1thì 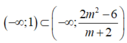
Hay 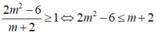
Kết hợp điều kiện m < -2 không có m
Vậy không có m thỏa mãn.