Cho f là một hàm số. Tìm số thực a > 0 sao cho ∀ x > 0

∫ a x f t t 2 d t + 6 = 2 x

A. 7

B. 8

C. 9

D. 10

Cho hàm số  

f(x)= x 2 + 4 - 2 x 2 khi   x ≠ 0 2 a - 5 4 khi   x = 0

Tìm giá trị thực của tham số a để hàm số f(x) liên tục tại x=0

A. a= -3/4

B. a= 4/3

C. a= -4/3

D. a= 3/4

Cho F(x) là một nguyên hàm của hàm số f ( x ) = x x + 1 .Tìm F(x) biết F(0)=0. 

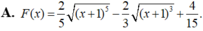
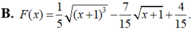
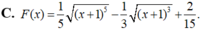
Cho F ( x ) là một nguyên hàm của hàm số f x = x x + 1 . Tìm F ( x ) biết  F ( 0 ) = 0

A. F x = 2 5 x + 1 5 − 2 3 x + 1 3 + 4 15

B.  F x = 1 5 x + 1 5 − 1 3 x + 1 3 + 2 15

C.  F x = 1 5 x + 1 3 − 7 15 x + 1 + 4 15

D.  F x = 2 5 x + 1 3 − 2 3 x + 1 + 4 15

Cho hàm số f x = x 2 + 4 − 2 x 2 k h i x ≠ 0 2 a − 5 4      ​  khi x = 0 .  Tìm giá trị thực của tham số a để hàm số f(x) liên tục tại x = 0  

A.  a = - 3 4

B. a = 4 3

C. a = - 4 3

D. a = 3 4

Cho số thực a>0. Giả  sử hàm số f(x) liên tục và luôn dương trên đoạn [0;a] thỏa mãn f(x).f(a – x) = 1, ∀ x ∈ [0;a]. Tính tích phân  I = ∫ 0 a 1 1 + f ( x ) d x

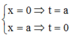
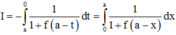
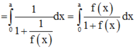
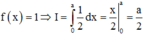
Cho F(x) là một nguyên hàm cùa hàm số  f ( x ) = x + sin x và f ( 0 ) = 1 . Tìm F(x)

A.  f x = x 2 2 - cos x + 2

B.  f x = x 2 2 - cos x - 2

C.  f x = x 2 2 + cos x

D.  f x = x 2 2 + cos x + 1 2