Cho a, b là các số thực dương thỏa mãn a ≠ 0 ; a ≠ b . Mệnh đề nào sau đây đúng?
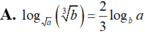
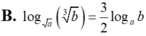
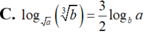
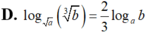
Cho a, b là các số thực dương thỏa mãn log 2 a + log 2 b = 0.
Cho a, b là các số thực dương thỏa mãn a ≢ 0 , a ≢ b . Mệnh đề nào sau đây đúng?
A. log a b 3 = 2 3 log b a
B. log a b 3 = 3 2 log a b
C. log a b 3 = 3 2 log b a
D. log a b 3 = 2 3 log a b
Đáp án D.
log a b 3 = log a 1 2 b 1 3 = 2 3 log a b
Cho a, b là các số thực dương thỏa mãn a ≠ 0 , a ≠ b . Mệnh đề nào sau đây đúng?
A. log a b 3 = 2 3 log b a
B. log a b 3 = 3 2 log a b
C. log a b 3 = 3 2 log b a
D. log a b 3 = 2 3 log a b
cho các số thực a, b , c thỏa mãn a+b+c >0; ab+bc+ca>0 và abc>0, CMR a,b,c là các số dương
Giả sử a<0,vì abc>0 nên bc<0.Mặt khác thì ab+ac+bc>0<=>a(b+c)>-bc>0=>a(b+c)>0,mà a<0 nên b+c<0=>a+b+c<0(vô lý).Vậy điều giả sử trên là sai,
a,b,c là 3 số dương.
Giả sử a<0,vì abc>0 nên bc<0.Mặt khác thì ab+ac+bc>0<=>a(b+c)>-bc>0=>a(b+c)>0,mà a<0 nên b+c<0=>a+b+c<0(vô lý).
Vậy điều giả sử trên là sai,
Do đó a,b,c là 3 số dương.
Cho a, b là các số thực dương thỏa mãn log 2 a + log 2 b = 0. Khẳng định nào sau đây đúng?
A. a + b = 2
B. a + b = 1
C. ab=1
D. ab=2
Cho a;b;c là ba số thực dương, a > 1 và thỏa mãn log 2 a b c + log a b 3 c 3 + b c 4 2 + 4 + 4 - c 2 = 0 . Số bộ a;b;c thỏa mãn điều kiện đã cho là:
A. 0
B. 1
C. 2
D. vô số
Ta có:

Dấu “=” xảy ra khi và chỉ khi


Vậy số bộ a,b,c thỏa mãn điều kiện đã cho là 1.
Chọn B.
Cho a,b là các số thực dương thỏa mãn a2 -2ab -3b2 ≥ 0. Tìm giá trị nhỏ nhất P =\(\dfrac{4a^2+b^2}{ab}\)
Lời giải:
$a^2-2ab-3b^2\geq 0$
$\Leftrightarrow (a^2+ab)-(3ab+3b^2)\geq 0$
$\Leftrightarrow a(a+b)-3b(a+b)\geq 0$
$\Leftrightarrow (a+b)(a-3b)\geq 0$
$\Leftrightarrow a-3b\geq 0$ (do $a+b>0$ với mọi $a,b>0$)
$\Leftrightarrow a\geq 3b$
Xét hiệu:
$P-\frac{37}{3}=\frac{4a^2+b^2}{ab}-\frac{37}{3}$
$=\frac{12a^2+3b^2-37ab}{3ab}=\frac{(a-3b)(12a-b)}{3ab}\geq 0$ do $a\geq 3b>0$
$\Rightarrow P\geq \frac{37}{3}$
Vậy $P_{\min}=\frac{37}{3}$
Cho a, b, x, y là các số thực dương thỏa mãn a ≠ 1 , b ≠ 1 , x 2 + y 2 = 1. Biết rằng log a x + y > 0 và log b x y < 0 . Mệnh đề nào sau đây đúng?
A. 0 < a < 1 v à b > 1
B. a > 1 v à b > 1
C. 0 < a < 1 v à 0 < b < 1
D. a > 1 v à 0 < b < 1
Các Ctv hoặc các giáo viên helpp ạ
Cho a,b,c là số thực dương không âm thỏa mãn
Cho a,b,c là số thực dương không âm thỏa mãn \(a+b+c=1\) . Chứng minh rằng :
\(\dfrac{1}{a^2+b^2}+\dfrac{1}{b^2+c^2}+\dfrac{1}{c^2+a^2}>10\)