Có bao nhiêu giá trị nguyên âm lớn hơn -9 của tham số m để phương trình 2 cos x - 1 2 cos 2 x + 2 cos x - m = 3 - 4 sin 2 x
có hai nghiệm thuộc đoạn - π 2 ; π 2
A. 6
B. 5
C. 1
D. 4
Có bao nhiêu giá trị nguyên của tham số m để phương trình 1 + 2 cos x + 1 + 2 sin x = 1 2 m có nghiệm?
A. 3.
B. 5.
C. 4.
D. 2.
Có bao nhiêu giá trị nguyên của tham số m để phương trình
m + 3 . m + cos x 3 3 = cos x có nghiệm thực?
A. 2.
B. 7.
C. 5.
D. 3.
Có bao nhiêu giá trị nguyên của tham số m để phương trình sin 2 x + cos 2 x + | sin x + cos x | - cos 2 x + m - m = 0 có nghiệm thực?
A. 9
B. 2
C. 3
D. 5
Đáp án C
Sử dụng tính đơn điệu của hàm số, đánh giá số nghiệm của phương trình.
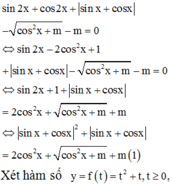
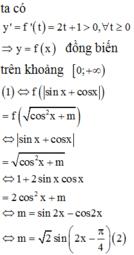

Vậy, có 3 giá trị nguyên của m thỏa mãn yêu cầu đề bài.
Có bao nhiêu giá trị nguyên của tham số m để phương trình cos 3 x - cos 2 x + m cos x = 1 có đúng 7 nghiệm khác nhau thuộc khoảng - π 2 ; 2 π
A. 2
B. 4
C. Không tồn tại
D. 1
Chọn D.
Phương pháp: Biện luận nghiệm của phương trình theo m.
Cách giải: Ta có:
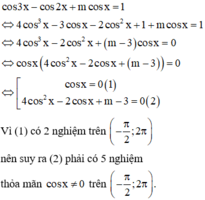

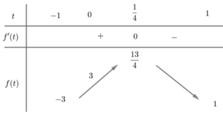

Cho phương trình m. sin x + 4. cos x = 2m - 5 với m là tham số. Có bao nhiêu giá trị nguyên của m để phương trình có nghiệm?
A. 4
B. 7.
C. 6.
D. 5
Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình -x2-4x = m+3 có hai nghiệm âm phân biệt?
ta có phương trình như sau :
\(x^2+4x+m+3=0\text{ có hai nghiệm âm phân biệt}\Leftrightarrow\)\(\hept{\begin{cases}\Delta'>0\\S< 0\\P>0\end{cases}}\Leftrightarrow\hept{\begin{cases}4-m-3>0\\-4< 0\\m+3>0\end{cases}}\Leftrightarrow1>m>-3\)
vậy có 3 giá trị nguyên của m là 0,-1, -2
Có bao nhiêu giá trị nguyên của tham số m thuộc \(\left[-10;10\right]\) để phương trình: 23m.7\(x^2-2x\) + 73m.2\(x^2-2x\) =143m(7x2 -14x +2 -7.3m) có 4 nghiệm phân biệt trong đó có đúng hai nghiệm lớn hơn -1
Đề hình như hơi sai sai ở chỗ \(-7.3^m\) cuối cùng
Đúng như vầy thì chắc ko làm được đâu, \(-7.3m\) mới có cơ hội biến đổi
Xét \(I_1=\int\limits^{\dfrac{\pi}{2}}_0f\left(sinx\right)dx\)
Đặt \(x=\pi-t\Rightarrow dx=-dt\) ; \(sinx=sin\left(\pi-t\right)=sint\)
\(\left\{{}\begin{matrix}x=0\Rightarrow t=\pi\\x=\dfrac{\pi}{2}\Rightarrow t=\dfrac{\pi}{2}\end{matrix}\right.\)
\(\Rightarrow I_1=\int\limits^{\dfrac{\pi}{2}}_{\pi}f\left(sint\right).\left(-dt\right)=\int\limits^{\pi}_{\dfrac{\pi}{2}}f\left(sint\right)dt=\int\limits^{\pi}_{\dfrac{\pi}{2}}f\left(sinx\right)dx\)
\(\Rightarrow4042=2I_1=\int\limits^{\dfrac{\pi}{2}}_0f\left(sinx\right)dx+\int\limits^{\pi}_{\dfrac{\pi}{2}}f\left(sinx\right)dx=\int\limits^{\pi}_0f\left(sinx\right)dx\)
Xét \(I_2=\int\limits^{\pi}_0x.f\left(sinx\right)dx\)
Đặt \(x=\pi-t\Rightarrow dx=-dt;sinx=sint\) ; \(\left\{{}\begin{matrix}x=0\Rightarrow t=\pi\\x=\pi\Rightarrow t=0\end{matrix}\right.\)
\(I_2=\int\limits^0_{\pi}\left(\pi-t\right)f\left(sint\right)\left(-dt\right)=\int\limits^{\pi}_0\left(\pi-t\right)f\left(sint\right)dt=\int\limits^{\pi}_0\left(\pi-x\right)f\left(sinx\right)dx\)
\(=\pi\int\limits^{\pi}_0f\left(sinx\right)dx-\int\limits^{\pi}_0x.f\left(sinx\right)dx=4042\pi-I_2\)
\(\Rightarrow2I_2=4042\pi\Rightarrow I_2=2021\pi\)
Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 2021 để phương trình \(4x^2+\left(3-2m\right)x+1+2\sqrt{4x^3+x}=0\) có nghiệm
ĐKXĐ: \(x\ge0\)
- Với \(x=0\) không phải nghiệm
- Với \(x>0\) , chia 2 vế của pt cho \(x\) ta được:
\(\dfrac{4x^2+1}{x}+2\sqrt{\dfrac{4x^2+1}{x}}+3-2m=0\)
Đặt \(t=\sqrt{\dfrac{4x^2+1}{x}}\ge\sqrt{\dfrac{2\sqrt{4x^2}}{x}}=2\)
Pt trở thành: \(t^2+2t+3-2m=0\)
\(\Leftrightarrow t^2+2t+3=2m\) (1)
Pt đã cho có nghiệm khi và chỉ khi (1) có nghiệm \(t\ge2\)
Xét hàm \(f\left(t\right)=t^2+2t+3\) khi \(t\ge2\)
Do \(\left\{{}\begin{matrix}a=1>0\\-\dfrac{b}{2a}=-1< 2\end{matrix}\right.\) \(\Rightarrow f\left(t\right)\) đồng biến khi \(t\ge2\)
\(\Rightarrow f\left(t\right)\ge f\left(2\right)=11\)
\(\Rightarrow\) Pt có nghiệm khi \(2m\ge11\Rightarrow m\ge\dfrac{11}{2}\)