Cho hàm số ![]() có đồ thị
có đồ thị ![]() . Phương trình tiếp tuyến của đồ thị
. Phương trình tiếp tuyến của đồ thị ![]() tại tiếp điểm có hoành độ bằng 1 là:
tại tiếp điểm có hoành độ bằng 1 là:
A. ![]() .
.
B. ![]() .
.
C.![]() .
.
D. ![]() .
.
Cho hàm số y = f x có đạo hàm trên R và đồ thị C . Tiếp tuyến của đồ thị C tại điểm 2 ; m có phương trình là y = 4 x - 6 . Tiếp tuyến của các đồ thị hàm số y = f f x và y = f 3 x 2 - 10 tại điểm có hoành độ bằng 2 có phương trình lần lượt là y = a x + b và y = c x + d . Tính giá trị của biểu thức S = 4 a + 3 c - 2 b + d .
A. S = -26
B. S = 176
C. S = 178
D. S = 174
Cho hàm số y = f(x) có đạo hàm trên R và đồ thị (C). Tiếp tuyến của đồ thị (C) tại điểm (2;m) có phương trình là y = 4 x - 6 . Tiếp tuyến của các đồ thị hàm số y = f f x và y = f 3 x 2 - 10 tại điểm có hoành độ bằng 2 có phương trình lần lượt là y = a x + b v à y = c x + d . Tính giá trị của biểu thức S = 4 a + 3 c - 2 b + d
A. S = -26
B. S = 176
C. S = 178
D. S = 174
a) tìm hệ số góc của tiếp tuyến của đồ thị hàm số y=-x^3+3x-2 (c) tại điểm có hoành độ -3
b) viết phương trình tiếp tuyến của đồ thị hàm số (c) trên tại điểm ( ứng với tiếp điểm ) có hoành độ -3
Cho hàm số y=f(x)=-x3+x2-1 có đồ thị (C):
Viết phương trình tiếp tuyến với đồ thị của hàm số tại điểm có hoành độ bằng 2
f'(x)=y'=-3x^2+2x
f'(2)=-3*2^2+2*2=-3*4+4=-8
f(2)=-2^3+2^2-1=-8-1+4=-9+4=-5
y=f(2)+f'(2)(x-2)
=-5+(-8)(x-2)
=-8x+16-5
=-8x+11
Đề bài
Cho hàm số \(y = - 2{x^2} + x\) có đồ thị (C).
a) Xác định hệ số góc của tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 2
b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm M(2; - 6)
a, Hệ số góc của tiếp tuyến của đồ thị là:
\(y'\left(2\right)=-4\cdot2+1=-7\)
b, Phương trình tiếp tuyến của đồ thị (C) tại điểm M(2;-6) là:
\(y=y'\left(2\right)\cdot\left(x-2\right)-6=-7\left(x-2\right)-6=-7x+8\)
Cho hàm số y = ln x 2 có đồ thị (C). Tiếp tuyến của đồ thị (C) tại điểm có hoành độ x 0 = e có phương trình là
A. y = 2 e x + 4 .
B. y = 2 e x + 3 .
C. y = 2 e x
D. y = 2 e x − 2 .
Phương trình tiếp tuyến của đồ thị hàm số ![]() tại điểm có hoành độ bằng 1 là:
tại điểm có hoành độ bằng 1 là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Chọn B
Đặt ![]()
ta có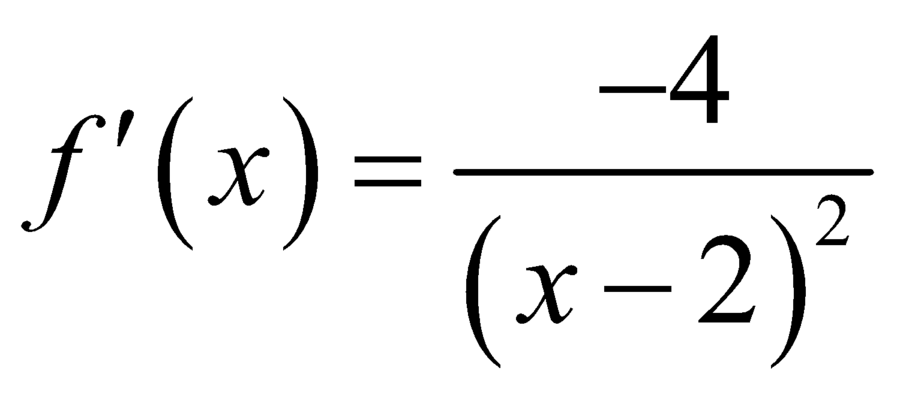 .
.
Với ![]() ta có
ta có ![]() .
.
Vậy tiếp điểm là ![]() .
.
Hệ số góc của tiếp tuyến là: 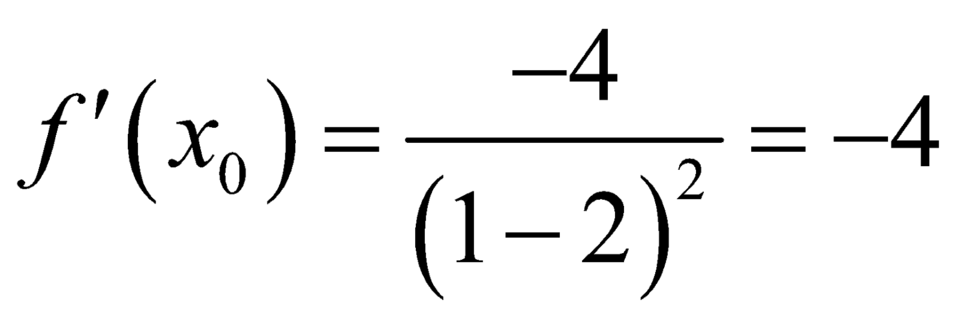 .
.
Phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm ![]() là:
là:
![]()
![]()
![]() .
.
Vậy phương trình tiếp tuyến cần tìm là ![]() .
.
Phương trình tiếp tuyến của đồ thị hàm số ![]() tại điểm có hoành độ bằng -1 là
tại điểm có hoành độ bằng -1 là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y = x 3 − 3 x 2 + 2 có đồ thị (C). Tiếp tuyến của (C) tại điểm có hoành độ bằng 1 có phương trình là
A. y = − 3 x
B. y = 3 x − 3
C. y = 3 x
D. y = − 3 x + 3
Đáp án A
Ta có: S A B C = 1 2 a 2 sin 60 ∘ = a 2 3 4 . Thể tích của lăng trụ ABC.A'B'C' là:
V = A A ' . S A B C = 2 a . a 2 3 4 = a 2 3 2 .