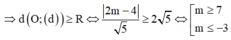Cho số phức z = m - 2 + ( m 2 - 1 ) i , với m là tham số thực thay đổi. Tập hợp các điểm biểu diễn số phức z nằm trên đường cong (C). Tính diện tích hình phẳng giới hạn bởi (C) và trục hoành.
A. 1 3
B. 8 3
C. 4 3
D. 2 3
Cho số phức z = m + 3 + ( m 2 - 1 ) i , với m là tham số thực thay đổi. Tập hợp các điểm biểu diễn số phức z thuộc đường cong (C). Tính diện tích hình phẳng giới hạn bởi (C) và trục hoành.
A. 4 3
B. 8 3
C. 2 3
D. 1 3
Cho số phức z = m + 3 + ( m 2 - 1 ) i với m là tham số thực thay đổi. Tập hợp các điểm biểu diễn số phức z thuộc đường cong (C). Tính diện tích hình phẳng giới hạn bởi (C) và trục hoành.
A. 4/3
B. 8/3
C. 2/3
D. 1/3
Trên tập ℂ , cho số phức z = i + m i - 1 với m là tham số thực khác -1. Tìm tất cả các giá trị của tham số m để z. z ¯ = 5
A. m = -3
B. m = 1
C. m = ± 2
D. m = ± 3
Trên tập ℂ , cho số phức z = i + m i - 1 với m là tham số thực khác -1. Tìm tất cả các giá trị của tham số m để z. z ¯ = 5
A. m = -3
B. m = 1
C. m = ± 2
D. m = ± 3
Cho số phức z = m + m 3 - m i với m là tham số thực thay đổi. Tập hợp tất cả các điểm biểu diễn số phức z là đường cong (C). Tính diện tích hình phẳng giới hạn bởi (C) và trục hoành.
A. 1 2
B. 1 4
C. 3 4
D. 3 2
Trên tập ℂ , cho số phức z = i + m i − 1 , với m là tham số thực khác -1. Tìm tất cả các giá trị của tham số m để z . z ¯ = 5.
A. m = − 3.
B. m = 1.
C. m = ± 2.
D. m = ± 3.
Đáp án D.
Ta có z . z ¯ = 5 ⇔ z 2 = 5 ⇔ m 2 + 1 2 = 5 ⇔ m 2 = 9 ⇔ m = ± 3.
Cho số phức z thỏa mãn 1 + i z là số thực và |z-2|=m với m ∈ R. Gọi m 0 là một giá trị của m để có đúng một số phức thỏa mãn bài toán. Khi đó
A. m 0 ∈ ( 0 ; 1 / 2 )
B. m 0 ∈ ( 1 / 2 ; 1 )
C. m 0 ∈ ( 3 / 2 ; 2 )
D. m 0 ∈ ( 1 ; 3 / 2 )
Cho số thực a thay đổi và số phức z thỏa mãn z a 2 + 1 = i - a 1 - a a - 2 i . Trên mặt phẳng tọa độ, gọi M là điểm biểu diễn số phức z . Khoảng cách giữa hai điểm M và I (-3; 4) (khi a thay đổi) là:
A. 4
B. 3
C. 5
D. 6
Cho hai số phức z, ω thỏa mãn z - 1 = z + 3 - 2 i ; ω = z + m + i với m ∈ ℝ là tham số. Giá trị của m để ta luôn có là
A. 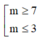
B. 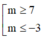
C. 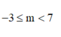
D. 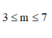
Đáp án B
Ta có:

Tập hợp điểm M biểu diễn w là trung trực của ![]() nên là đường thẳng d qua trung điểm I(m-1;2) và có
n
→
(
4
;
-
2
)
nên là đường thẳng d qua trung điểm I(m-1;2) và có
n
→
(
4
;
-
2
)
![]()
Đặt ![]()
Do ω ⩾ 2 5 nên M nằm ngoài đường tròn tâm O bán kính R= 2 5