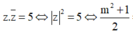Các câu hỏi tương tự
Trên tập
ℂ
, cho số phức z
i
+
m
i
-
1
với m là tham số thực khác -1. Tìm tất cả các giá trị của tham số m để z.
z
¯
5 A. m -3 B. m 1 C. m
±
2 D. m
±
3
Đọc tiếp
Trên tập ℂ , cho số phức z = i + m i - 1 với m là tham số thực khác -1. Tìm tất cả các giá trị của tham số m để z. z ¯ = 5
A. m = -3
B. m = 1
C. m = ± 2
D. m = ± 3
Gọi S là tập hợp tất cả các giá trị thực của tham số m để tồn tại duy nhất số phức z thỏa mãn z.
z
¯
1 và |z -
3
+ i|. Tìm số phần tử của S A. 1. B. 2. C. 3. D. 4
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị thực của tham số m để tồn tại duy nhất số phức z thỏa mãn z. z ¯ = 1 và |z - 3 + i|. Tìm số phần tử của S
A. 1.
B. 2.
C. 3.
D. 4
Cho hai số phức z,
ω
thỏa mãn
z
-
1
z
+
3
-
2
i
;
ω
z
+...
Đọc tiếp
Cho hai số phức z, ω thỏa mãn z - 1 = z + 3 - 2 i ; ω = z + m + i với m ∈ ℝ là tham số. Giá trị của m để ta luôn có là
A. 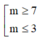
B. 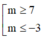
C. 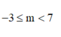
D. 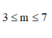
Tìm tập hợp tất cả các giá trị của tham số m để có đúng 8 số phức z thỏa mãn đồng thời các điều kiện
z
+
z
¯
+
z
-
z
¯
z
2
và
z
m
Đọc tiếp
Tìm tập hợp tất cả các giá trị của tham số m để có đúng 8 số phức z thỏa mãn đồng thời các điều kiện z + z ¯ + z - z ¯ = z 2 và z = m
![]()
![]()
![]()
![]()
Cho số phức
z
m
+
3
+
(
m
2
-
1
)
i
với m là tham số thực thay đổi. Tập hợp các điểm biểu diễn số phức z thuộc đường cong (C). Tính diện tích hình phẳng giới hạn bởi (C) và trục hoành. A. 4/3 B. 8/3 C. 2/3 D. 1/3
Đọc tiếp
Cho số phức z = m + 3 + ( m 2 - 1 ) i với m là tham số thực thay đổi. Tập hợp các điểm biểu diễn số phức z thuộc đường cong (C). Tính diện tích hình phẳng giới hạn bởi (C) và trục hoành.
A. 4/3
B. 8/3
C. 2/3
D. 1/3
Gọi A, B là hai điểm cực trị của đồ thị hàm số f(x) = x3 - 3x2 + m với m là tham số thực khác 0. Tìm tất cả các giá trị thực của tham số m để trọng tâm tam giác OAB thuộc đường thẳng 3x + 3y - 8 = 0.
A. m = 5
B. m = 2
C. m = 6
D. m = 4
Cho số phức
z
m
+
m
3
-
m
i
với m là tham số thực thay đổi. Tập hợp tất cả các điểm biểu diễn số phức z là đường cong (C). Tính diện tích hình phẳng giới hạn bởi (C) và trục hoành. A.
1
2
B.
1
4
C....
Đọc tiếp
Cho số phức z = m + m 3 - m i với m là tham số thực thay đổi. Tập hợp tất cả các điểm biểu diễn số phức z là đường cong (C). Tính diện tích hình phẳng giới hạn bởi (C) và trục hoành.
A. 1 2
B. 1 4
C. 3 4
D. 3 2
Cho số phức
z
a
+
b
i
a
,
b
∈
R
Biết tập hợp các điểm A biểu diễn hình học số phức z là đường tròn (C) có tâm I(4;3) và bán kính R3 Đặt M là giá trị lớn nhất, m là giá trị nhỏ nhất của F 4a+3b-1 Tính giá trị M+m A. M + m 63 B. M + m 48 C. M + m 50 D. M + m 41
Đọc tiếp
Cho số phức z = a + b i a , b ∈ R Biết tập hợp các điểm A biểu diễn hình học số phức z là đường tròn (C) có tâm I(4;3) và bán kính R=3 Đặt M là giá trị lớn nhất, m là giá trị nhỏ nhất của F = 4a+3b-1 Tính giá trị M+m
A. M + m = 63
B. M + m = 48
C. M + m = 50
D. M + m = 41
Cho số phức z a + bi(a,b
∈
ℝ
). Biết tập hợp các điểm A biểu diễn hình học số phức z là đường tròn (C) có tâm I(4;3) và bán kính R 3 . Đặt M là giá trị lớn nhất, m là giá trị nhỏ nhất của F 4a + 3b -1. Tính giá trị M + m A. M + m 63 B. M + m 48 C. M + m 50 D. M + m 41
Đọc tiếp
Cho số phức z = a + bi(a,b ∈ ℝ ). Biết tập hợp các điểm A biểu diễn hình học số phức z là đường tròn (C) có tâm I(4;3) và bán kính R = 3 . Đặt M là giá trị lớn nhất, m là giá trị nhỏ nhất của F = 4a + 3b -1. Tính giá trị M + m
A. M + m = 63
B. M + m = 48
C. M + m = 50
D. M + m = 41