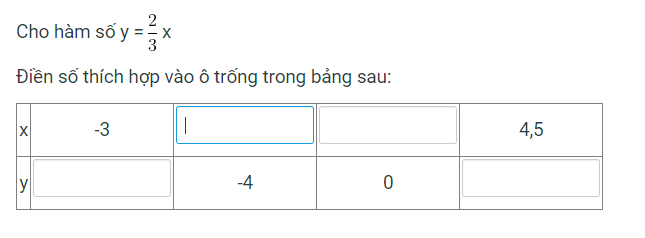
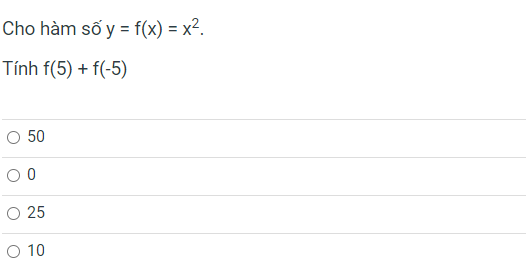mình dg cần gấp ạ
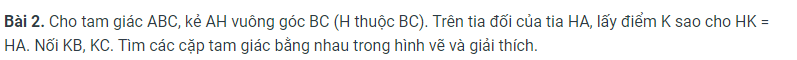
mình dg cần gấp ạ
Mình dg cần gấp ạ
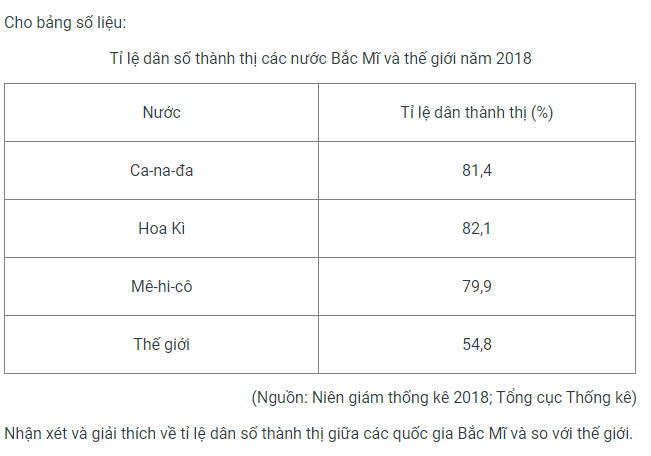
Nhận xét: Tỉ lệ dân số sống ở thành thị ở Bắc Mĩ cao hơn so với thế giới.
Nguyên nhân: Dân cư tập trung ở vùng Ngũ Đại Hồ và Đông Bắc Hoa Kì do ở đây công nghiệp hóa sớm, mức độ đo thị hóa cao, có nhiều thành phố tiện nghi ở đó. Còn các vùng khác do địa hình và khí hậu không thuận lợi nên vùng đó thưa và ít dân.
- Tỉ lệ dân số thành thị giữa các quốc gia bắc mĩ cao hơn so với tỉ lệ trung bình thế giới
- Tỉ lệ dân số thành thị sẽ ngày càng tăng cao
- Nguyên nhân :
+ Do quy hoạch dân cư chưa tốt, làm tăng dân cư ở những nơi màu mỡ, nhiều khu công nghiệp.
+ Sự phát triển của khoa-học kĩ thuật, cách mạng công nghiệp hiện đại hóa làm cho máy móc tốt hơn, các khu công nghệ cao mọc lên nhiều hơn, cần nguồn nhân công dồi dào từ nhiều nơi → Nhiều công nhân lao động tập trung lại các khu công nghệ cao → thành thị đông dân ra đời.

cứu mình với mình dg cần gấp bây giờ ạ
Mình dg cần rất gấp luon ạ mog mn giúp đỡ
Bài 5:
Thay x=1 và y=2 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}-m\cdot1+2=-2m\\1+m^2\cdot2=9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2m=-m+2\\2m^2=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2=4\\-m=2\end{matrix}\right.\)
=>m=-2
Bài 6:
a: ĐKXĐ: x>=1 và y>=-2
\(\left\{{}\begin{matrix}\sqrt{x-1}-3\sqrt{y+2}=2\\2\sqrt{x-1}+5\sqrt{y+2}=15\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2\sqrt{x-1}-6\sqrt{y+2}=4\\2\sqrt{x-1}+5\sqrt{y+2}=15\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-11\sqrt{y+2}=-11\\\sqrt{x-1}-3\sqrt{y+2}=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{y+2}=1\\\sqrt{x-1}=2+3=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y+2=1\\x-1=25\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=26\\y=-1\end{matrix}\right.\left(nhận\right)\)
b: ĐKXĐ: x<>0 và y<>0
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\\\dfrac{8}{x}+\dfrac{15}{y}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{8}{x}+\dfrac{8}{y}=\dfrac{8}{12}=\dfrac{2}{3}\\\dfrac{8}{x}+\dfrac{15}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{7}{y}=\dfrac{-1}{3}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=21\\\dfrac{1}{x}=\dfrac{1}{12}-\dfrac{1}{21}=\dfrac{7-4}{84}=\dfrac{3}{84}=\dfrac{1}{28}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=28\\y=21\end{matrix}\right.\left(nhận\right)\)
c: ĐKXĐ: x<>0 và y<>2
\(\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{3}{y-2}=4\\\dfrac{4}{x}-\dfrac{1}{y-2}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{4}{x}+\dfrac{6}{y-2}=8\\\dfrac{4}{x}-\dfrac{1}{y-2}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{7}{y-2}=7\\\dfrac{2}{x}+\dfrac{3}{y-2}=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y-2=1\\\dfrac{2}{x}=4-\dfrac{3}{1}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.\left(nhận\right)\)
d: ĐKXĐ: x<>-2y và x<>-y/2
\(\left\{{}\begin{matrix}\dfrac{2}{x+2y}+\dfrac{1}{2x+y}=3\\\dfrac{4}{x+2y}-\dfrac{3}{2x+y}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{6}{x+2y}+\dfrac{3}{2x+y}=9\\\dfrac{4}{x+2y}-\dfrac{3}{2x+y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{10}{x+2y}=10\\\dfrac{4}{x+2y}-\dfrac{3}{2x+y}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+2y=1\\\dfrac{3}{2x+y}=4-1=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+2y=1\\2x+y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+4y=2\\2x+y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3y=1\\x+2y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{1}{3}\\x=1-\dfrac{2}{3}=\dfrac{1}{3}\end{matrix}\right.\left(nhận\right)\)
e: ĐKXĐ: x>4 và y<>-2
\(\left\{{}\begin{matrix}\dfrac{3}{\sqrt{x-4}}+\dfrac{4}{y+2}=7\\\dfrac{5}{\sqrt{x-4}}-\dfrac{1}{y+2}=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{3}{\sqrt{x-4}}+\dfrac{4}{y+2}=7\\\dfrac{20}{\sqrt{x-4}}-\dfrac{4}{y+2}=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{23}{\sqrt{x-4}}=23\\\dfrac{5}{\sqrt{x-4}}-\dfrac{1}{y+2}=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{x-4}=1\\\dfrac{1}{y+2}=5-4=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-4=1\\y+2=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=5\\y=-1\end{matrix}\right.\left(nhận\right)\)
f: ĐKXĐ: x>=-1
\(\left\{{}\begin{matrix}2\left(x+y\right)+\sqrt{x+1}=4\\\left(x+y\right)-\sqrt{x+1}=-5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2\left(x+y\right)+\sqrt{x+1}+\left(x+y\right)-\sqrt{x+1}=4-5=-1\\\left(x+y\right)-\sqrt{x+1}=-5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3\left(x+y\right)=-1\\\sqrt{x+1}=-\dfrac{1}{3}+5=\dfrac{14}{3}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+y=-\dfrac{1}{3}\\x+1=\dfrac{196}{9}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{187}{9}\\y=-\dfrac{1}{3}-\dfrac{187}{9}=-\dfrac{190}{9}\end{matrix}\right.\left(nhận\right)\)
Nhiều quá em, em chỉ nên đăng những câu nào cảm thấy khó khăn khi giải quyết thôi
Mik dg cần gấp ạ
mik dg cần gấp ạ
\(a,y=kx\Leftrightarrow8=6k\Leftrightarrow k=\dfrac{8}{6}=\dfrac{4}{3}\\ b,y=\dfrac{4}{3}x\\ c,x=12\Leftrightarrow y=\dfrac{4}{3}\cdot12=16\)
mik dg cần gấp ạ :(
| x | -4 | -2 | -1 | \(-\dfrac{1}{2}\) | 1 | \(\dfrac{3}{2}\) |
| y | 8 | 4 | 2 | 1 | -2 | -3 |
Mik dg cần gấp ạ!
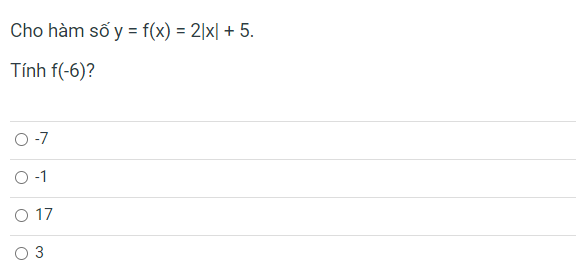
Mik dg cần gấp ạ