Cho a,b là các số thực thỏa mãn 0<a<b<1. Mệnh đề nào sau đây đúng
A. log a b > 1
B. log b a < 0
C. log a b > log b a
D. log b a > log a b
Cho a, b là các số thực dương thỏa mãn log 2 a + log 2 b = 0.
Cho a, b là các số thực dương thỏa mãn a ≢ 0 , a ≢ b . Mệnh đề nào sau đây đúng?
A. log a b 3 = 2 3 log b a
B. log a b 3 = 3 2 log a b
C. log a b 3 = 3 2 log b a
D. log a b 3 = 2 3 log a b
Đáp án D.
log a b 3 = log a 1 2 b 1 3 = 2 3 log a b
Cho a, b là các số thực dương thỏa mãn a ≠ 0 ; a ≠ b . Mệnh đề nào sau đây đúng?
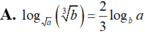
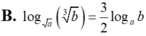
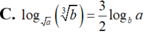
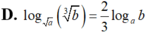
Cho a, b là các số thực dương thỏa mãn a ≠ 0 , a ≠ b . Mệnh đề nào sau đây đúng?
A. log a b 3 = 2 3 log b a
B. log a b 3 = 3 2 log a b
C. log a b 3 = 3 2 log b a
D. log a b 3 = 2 3 log a b
cho các số thực a, b , c thỏa mãn a+b+c >0; ab+bc+ca>0 và abc>0, CMR a,b,c là các số dương
Giả sử a<0,vì abc>0 nên bc<0.Mặt khác thì ab+ac+bc>0<=>a(b+c)>-bc>0=>a(b+c)>0,mà a<0 nên b+c<0=>a+b+c<0(vô lý).Vậy điều giả sử trên là sai,
a,b,c là 3 số dương.
Giả sử a<0,vì abc>0 nên bc<0.Mặt khác thì ab+ac+bc>0<=>a(b+c)>-bc>0=>a(b+c)>0,mà a<0 nên b+c<0=>a+b+c<0(vô lý).
Vậy điều giả sử trên là sai,
Do đó a,b,c là 3 số dương.
cho phương trình ax^2+bx+c=0 với các số a,b,c là các số thực nghiệm khác 0 và thỏa mãn điều kiện a+b+2c=0. Chứng minh rằng phương trình trên luôn có nghiệm trên tập số thực
Đặt \(f\left(x\right)=ax^2+bx+c\).
\(f\left(0\right)=c;f\left(1\right)=a+b+c\)
Do \(a+b+2c=0\) nên c và \(a+b+c\) trái dấu. Suy ra f(0)f(1) < 0 nên f(x) = 0 luôn có ít nhất 1 nghiệm tren (0; 1).
Cho a,b là các số thực thỏa mãn \(a^2+ab+b^2-b=0\).Chứng minh:
\(A=3a^5+b^4< 4\)
\(a^2+ab+b^2-b=0\)
\(\Delta=b^2-4\left(b^2-b\right)\ge0\Leftrightarrow-3b^2+4b\ge0\Rightarrow0\le b\le\dfrac{4}{3}\)
\(b^2+\left(a-1\right)b+a^2=0\)
\(\Delta=\left(a-1\right)^2-4a^2\ge0\Rightarrow-3a^2-2a+1\ge0\Rightarrow-1\le a\le\dfrac{1}{3}\)
\(\Rightarrow A=3a^5+b^4\le3.\left(\dfrac{1}{3}\right)^5+\left(\dfrac{4}{3}\right)^4=\dfrac{257}{81}< 4\)
Cho a, b là các số thực dương thỏa mãn log 2 a + log 2 b = 0. Khẳng định nào sau đây đúng?
A. a + b = 2
B. a + b = 1
C. ab=1
D. ab=2
cho a;b là các số thực thỏa mãn a^3-3a^2+5a-2014=0;b^3-3b^2+5b+2008=0.Tính a+b