Biết n ∈ ℤ + , n > 4 và thỏa mãn A n 0 0 ! + A n 1 1 ! + A n 2 2 ! + A n 3 3 ! + . . . + A n n n ! = 32 n - 4 Tính P = 1 n ( n + 1 )
A. 1 42
B. 1 30
C. 1 56
D. 1 72
Biết n ∈ ℤ + , n > 4 và thỏa mãn A n 0 0 ! + A n 1 1 ! + A n 2 2 ! + A n 3 3 ! + . . . + A n n n ! = 32 n - 4 . Tính P = 1 n n + 1
A. P = 1 42
B. P = 1 30
C. P = 1 56
D. P = 1 72
Cho số phức z = 1 + i n , biết n ∈ ℤ và thỏa mãn log 2 8 − n + log 2 n + 3 = log 2 10
Tính môđun của số phức z
A. 8
B. z = 8 2 hoặc z = 1 2
C. 4 2
D. 2
Cho số phức z = i + 1 n , biết n ∈ ℤ và thỏa mãn log 2 8 - n + log 2 n + 3 = log 2 10 .
Tính môđun của số phức z.
A. 2
B. 4 2
C. 8
D. z = 8 2 h o ặ c z = 1 2
Cho khai triển ( 1 + 2 x ) n = a 0 + a 1 x + a 2 x 2 + . . . + a n x n , trong đó n ∈ ℤ + . Biết các hệ số a 0 , a 1 , . . . , a n thỏa mãn hệ thức a 0 + a 1 2 + . . . + a n 2 n = 4096 . Hệ số a 8 bằng
A. 130272
B. 126720
C. 130127
D. 213013
Chọn B
Ta có: ![]()
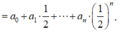
Trong khai triển ( 1 + 2 x ) n = a 0 + a 1 x + a 2 x 2 + . . . + a n x n thay x = 1 2 ta được
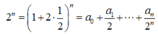
![]()
Số hạng tổng quát trong khai triển ![]()
Để có số hạng chứa x 8 thì k = 8.
Vậy ![]()
Cho m và n là số nguyên khác 0 thỏa mãn 4/m - 1/n = 1. Tìm m; n
Hôm nay olm sẽ hướng dẫn em giải bài này như sau
Biến đổi đưa bài toán trở thành dạng tìm điều kiện để phân số là một số nguyên em nhé
\(\dfrac{4}{m}\) - \(\dfrac{1}{n}\) = 1 ⇒ 4n - m = mn ⇒m + mn = 4n ⇒ m(1+n) = 4n
m = \(\dfrac{4n}{1+n}\) (n \(\ne\) 0; -1)
m \(\in\) Z ⇔ 4n ⋮ 1 + n ⇒ 4n + 4 - 4 ⋮ 1 + n ⇒ 4(n+1) - 4 ⋮ 1 + n
⇒ 4 ⋮ 1 + n ⇒ n + 1 \(\in\) { -4; -2; -1; 1; 2; 4}
⇒ n \(\in\) { -5; -3; -2; 0; 1; 3} vì n \(\ne\) 0 ⇒ n \(\in\){ -5; -3; -2; 1; 3}
⇒ m \(\in\){ 5; 6; 8; 2; 3}
Vậy các cặp số nguyên m; n thỏa mãn đề bài lần lượ là:
(m; n) =(5; -5); (6; -3); ( 8; -2); (2; 1); ( 3; 3)
Biết n ∈ Z + , n > 4 và thỏa mãn A n 0 0 ! + A n 1 1 ! + . . . + A n n n ! = 32 n - 4 Tính P = 1 n ( n + 1 )
A. P = 1 42
B. P = 1 30
C. P = 1 56
D. P = 1 72
Cho khai triển nhị thức Niuton x 2 + 2 n x n với n n ∈ ℕ , x > 0. Biết rằng số
hạng thứ 2 của khai triển bằng 98 và n thỏa mãn A n 2 + 6 C n 3 = 36 n Trong các giá trị x sau, giá trị nào thỏa mãn?
A. 3
B. 4
C. 1
D. 2
Cho hàm số f(x) liên tục trên R, f x ≠ 0 với mọi x và thỏa mãn f 1 = − 1 2 , f ' x = 2 x + 1 f 2 x . Biết f 1 + f 2 + ... + f 2019 = a b − 1 v ớ i a ∈ ℤ , b ∈ ℕ , a ; b = 1 . Khẳng định nào sau đây là sai?
A. a − b = 2019
B. ab > 2019
C. 2 a + b = 2022
D. b ≤ 2020
Phương pháp:
- Lấy nguyên hàm hai vế từ đẳng thức đạo hàm và kết hợp điều kiện tìm f(x)
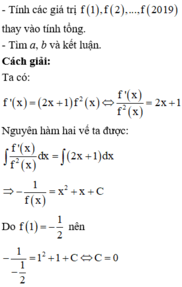

Cho tam giác ABC và đường thẳng d // BC cắt AB và AC tại M và N thỏa mãn AM = CN. Biết M(- 4 ; 0) ; C (5 ; 2). Chân đường phân giác trong góc A là D (0 ; -1). Tìm tọa độ hai điểm A và B