Cho khai triển ( 1 + 2 x ) 2019 = a 0 + a 1 x + a 2 x 2 + . . . . . + a n x n . Tính tổng các hệ số trong khai triển?
A. 2019
B. 3 2019
C. 3 2020
D. 2 2019
Những câu hỏi liên quan
cho đa thức F(x)= (2017x-2018)2019
khi khai triển ta đc đa thức bậc 2019
Tính tổng các hệ số của các số hạng của đa thức sau khi khai triển
3 tháng 10 2020 lúc 20:49
Xét khai triển (1+x)(1+2x)(1+3x)....(1+2019x) = a0 + a1x + a2x2 + a3x3 +...+ a2019x2019. Tính S = 2a2 + (11 + 22 +...+ 20192)
\(\left(1+x\right)\left(1+2x\right)...\left(1+nx\right)-1\)
\(=x+\sum\limits^n_{k=2}kx\left(1+x\right)...\left(1+\left(k-1\right)x\right)\)
\(=x+\sum\limits^n_{k=2}kx\left[\left(1+x\right)...\left(1+\left(k-1\right)x\right)-1+1\right]\)
\(=\sum\limits^n_{k=1}kx+\sum\limits^n_{k=2}kx\left[\left(1+x\right)\left(1+2x\right)...\left(1+\left(k-1\right)x\right)-1\right]\)
\(=\sum\limits^n_{k=1}kx+\sum\limits^n_{k=2}kx\left(\sum\limits^{k-1}_{i=1}ix\left(1+x\right)\left(1+2x\right)...\left(1-\left(i-1\right)x\right)\right)\)
Do đó tổng của các hệ số chứa \(x^2\) là: \(\sum\limits^n_{k=2}k\left(\sum\limits^{k-1}_{i=1}i\right)\)
Hay \(a_2=\sum\limits^n_{k=2}k\left(\frac{k\left(k-1\right)}{2}\right)=\sum\limits^n_{k=2}\frac{k^2\left(k-1\right)}{2}\)
Do đó:
\(S=1+\sum\limits^{2019}_{k=2}\frac{k^2\left(k-1\right)}{2}+\sum\limits^{2019}_{k=2}k^2=1+\sum\limits^{2019}_{k=2}\left(\frac{k^2\left(k-1\right)}{2}+k^2\right)\)
\(=1+\sum\limits^{2019}_{k=2}\left(\frac{k^2\left(k+1\right)}{2}\right)\)
(
x
+
2
)
n
+
5
,
(
n
∈
ℕ
)
Khai triển nhị thức có tất cả 2019 số hạng. Tìm n. A. 2018 B. 2014 C. 2013 D. 2015
Đọc tiếp
( x + 2 ) n + 5 , ( n ∈ ℕ ) Khai triển nhị thức có tất cả 2019 số hạng. Tìm n.
A. 2018
B. 2014
C. 2013
D. 2015
Chọn C
Khai triển ( x + 2 ) n + 5 , ( n ∈ ℕ ) có tất cả 2019 số hạng nên (n+5) + 1 = 2019 => n = 2013
Đúng 0
Bình luận (0)
Tính tổng các hệ số trong khai triển ( 1 - 2 x ) 2019
A. -1
B. 2019
C. -2019
D. 1
Chọn A
Đặt
(
1
-
2
x
)
2019
Cho x = 1 ta có tổng các hệ số 
Đúng 0
Bình luận (0)
Trong khai triển Newton của biểu thức
(
2
x
-
1
)
2019
, số hạng chứa
x
18
là
A
.
-
2
18
.
C
2019
18
.
B
.
2
18
....
Đọc tiếp
Trong khai triển Newton của biểu thức ( 2 x - 1 ) 2019 , số hạng chứa x 18 là
A . - 2 18 . C 2019 18 .
B . 2 18 . C 2019 18 .
C . 2 18 . C 2019 18 . x 18 .
D . - 2 18 . C 2019 18 . x 18 .
Chọn D
Số hạng tổng quát trong khai triển ( 2 x - 1 ) 2019 là
Theo đề bài ta có: 2019 - k = 18 => k = 2001.
Vậy trong khai triển biểu thức đã cho, số hạng chứa x 18 là:
Đúng 0
Bình luận (0)
Trong khai triển Newton của biểu thức
(
2
x
-
1
)
2019
, số hạng chứa
x
18
là A.
-
2
18
.
C
2019
18
B.
-
2
18
.
C
2019
18
.
x...
Đọc tiếp
Trong khai triển Newton của biểu thức ( 2 x - 1 ) 2019 , số hạng chứa x 18 là
A. - 2 18 . C 2019 18
B. - 2 18 . C 2019 18 . x 18
C. 2 18 . C 2019 18
D. 2 18 . C 2019 18 . x 18
Trong khai triển Newton của biểu thức
(
2
x
-
1
)
2019
, số hạng chứa
x
18
là.
A
.
-
2
18
.
C
2019
18
B
.
-
2
18
....
Đọc tiếp
Trong khai triển Newton của biểu thức ( 2 x - 1 ) 2019 , số hạng chứa x 18 là.
A . - 2 18 . C 2019 18
B . - 2 18 . C 2019 18 x 18
C . 2 18 . C 2019 18 x 18
D . 2 18 . C 2019 18
Chọn B
Ta có:
(
2
x
-
1
)
2019
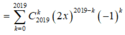
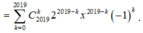
Số hạng tổng quát của khai triển là 
.
Để có x 18 thì 2019 - k = 18 => k = 2001.
Khi đó số hạng chứa
x
18
là 
.
Đúng 0
Bình luận (0)
Cho khai triển (2x-1)^6.(3x^2+1)^5 . Tìm số hạng chứa x^4 trong khai triển .
\(\left(2x-1\right)^6\left(3x^2+1\right)^5=\sum\limits^6_{k=0}C_6^k\left(2x\right)^k\left(-1\right)^{6-k}\sum\limits^5_{i=0}C_5^i\left(3x^2\right)^i\)
\(=\sum\limits^6_{k=0}\sum\limits^5_{i=0}C_6^k.C_5^i.\left(-1\right)^{6-k}.2^k.3^i.x^{k+2i}\)
Số hạng chứa \(x^4\) thỏa mãn:
\(\left\{{}\begin{matrix}0\le k\le6\\0\le i\le5\\k+2i=4\end{matrix}\right.\) \(\Rightarrow\left(i;k\right)=\left(0;4\right);\left(1;2\right);\left(2;0\right)\)
Hệ số:
\(C_6^4.C_5^0\left(-1\right)^4.2^4.3^0+C_6^2C_5^1\left(-1\right)^2.2^2.3^1+C_6^0.C_5^2.\left(-1\right)^0.2^0.3^2=...\)
Đúng 0
Bình luận (0)
23 tháng 4 2023 lúc 9:50
1. Hệ số của x^5 trong khai triển xleft(1-xright)^4+x^2left(1-2xright)^4 là:A. 1 B. 24 C. 32 D. -312. Cho khai triển left(1+2xright)^5a_0+a_1x+a_2x^2+...+a_5x^5. Tính tổng các hệ số trong khai triển trên?A. 5 B. 243 C. 256 D. 13. Hệ số của số hạng thứ ba trong khai triển left(x-1right)^5 là:A. 1 B. 5 C. 12 ...
Đọc tiếp
1. Hệ số của \(x^5\) trong khai triển \(x\left(1-x\right)^4+x^2\left(1-2x\right)^4\) là:
A. 1 B. 24 C. 32 D. -31
2. Cho khai triển \(\left(1+2x\right)^5=a_0+a_1x+a_2x^2+...+a_5x^5.\) Tính tổng các hệ số trong khai triển trên?
A. 5 B. 243 C. 256 D. 1
3. Hệ số của số hạng thứ ba trong khai triển \(\left(x-1\right)^5\) là:
A. 1 B. 5 C. 12 D.10
