Chọn B
Ta có ![]()
![]()
Tổng các hệ số trong khai triển là: ![]()
Cho x = 1 ta có: ![]()
![]()
![]()
![]()
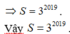
Chọn B
Ta có ![]()
![]()
Tổng các hệ số trong khai triển là: ![]()
Cho x = 1 ta có: ![]()
![]()
![]()
![]()
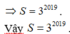
Tính tổng các hệ số trong khai triển ( 1 - 2 x ) 2019
A. -1
B. 2019
C. -2019
D. 1
( x + 2 ) n + 5 , ( n ∈ ℕ ) Khai triển nhị thức có tất cả 2019 số hạng. Tìm n.
A. 2018
B. 2014
C. 2013
D. 2015
Biết rằng trong khai triển trên tổng hệ số của ba số hạng đầu bằng 161. Tìm a
Gọi x là hệ số không chứa x trong khai triển nhị thức Niu – tơn
x 2 - 2 x n = C n 0 x 2 n + C n 1 x 2 n - 1 - 2 x + . . . + C n n - 1 x 2 - 2 x n - 1 + C n n - 2 x n n ∈ ℕ *
Biết rằng trong khai triển trên tổng hệ số của ba số hạng đầu bằng 161. Tìm a
A. 11520
B. 11250
C. 12150
D. 10125
Trong khai triển Newton của biểu thức ( 2 x - 1 ) 2019 , số hạng chứa x 18 là
A . - 2 18 . C 2019 18 .
B . 2 18 . C 2019 18 .
C . 2 18 . C 2019 18 . x 18 .
D . - 2 18 . C 2019 18 . x 18 .
Trong khai triển Newton của biểu thức ( 2 x - 1 ) 2019 , số hạng chứa x 18 là.
A . - 2 18 . C 2019 18
B . - 2 18 . C 2019 18 x 18
C . 2 18 . C 2019 18 x 18
D . 2 18 . C 2019 18
Giá trị của k để hàm só f(x)=\(\hept{\begin{cases}\frac{x^{2019}+x-2}{\sqrt{2020+1}-\sqrt{x+2020}}\\2k\end{cases}}\) liên tục tại x0=1 có dạng \(k=\frac{a\sqrt{b}}{c}\), với a,b,c là các số nguyên và \(\frac{a\sqrt{b}}{c}\)
là phân số tới giản. tính a-b+c ( f(x) = 2k , khi x<=1; f(x)=... khi x>1)
Cho số nguyên n ≥ 3 . Giả sử ta có khai triển
x - 1 2 n + x x + 1 2 n - 1 = a 0 + a 1 x + a 2 x 2 + . . . + a 2 n x 2 n . Biết rằng tổng a + a 2 + . . . + a 2 n - 2 + a 2 n = 768 . Tính a 5
A. 294
B. -126
C. 378
D. -84
Gọi a là hệ số của x 5 3 trong khai triển x 2 3 + 2 x 3 n , x > 0 biết rằng 2 n - 4 C n n - 2 - C n - 2 1 - n = C n - 1 n - 2
A. a = 96069
B. a = 96906
C. a = 96960
D. a = 96096
1/ Giải phương trình sau:
\(tan^2\left(x+\dfrac{\pi}{3}\right)+\left(\sqrt{3}-1\right)tan\left(x+\dfrac{\pi}{3}\right)-\sqrt{3}=0\)
2/ Tìm hệ số của số hạng chứa \(x^{26}\) trong khai triển \(\left(\dfrac{1}{x^4}+x^7\right)^n\) . Biết \(C^2_{n+2}-4C^n_{n+1}=2\left(n+1\right)\) (n ∈ N* ; x > 0)