Đáp án C

2 − x n = ∑ k = 0 n C n k − x k .2 n − k ⇒  hệ số của x 4  là: C n 4 − 1 4 .2 n − 4 = 280 ⇔ n = 7  

Chọn C

Khai triển  ( x + 2 ) n + 5 ,   ( n ∈ ℕ )  có tất cả 2019 số hạng nên (n+5) + 1 = 2019 => n = 2013

2/ \(\left(a+b\right)^k\Rightarrow k+1\left(so-hang\right)\)

\(\Rightarrow n+6+1=17\Rightarrow n=10\)

6/ \(\left(2a-1\right)^6=\sum\limits^6_{k=0}C^k_6.2^{6-k}.\left(-1\right)^k.a^{6-k}\)

\(\Rightarrow tong-3-so-hang-dau=C^0_6.2^6+C^1_6.2^5.\left(-1\right)+C^2_6.2^4.\left(-1\right)^2=...\)

7/ \(\left(x-\sqrt{y}\right)^{16}=\left(x-y^{\dfrac{1}{2}}\right)^{16}\)

\(\Rightarrow tong-2-so-hang-cuoi=C^{16}_{16}+C^{15}_{16}=...\)

Chọn D

Ta có, .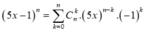

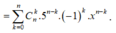Tổng các hệ số trong khai triển  ( 5 x - 1 ) n  bằng  2 100  nên ta có phương trình:

.

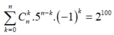
Vậy ( 5 x - 1 ) n .

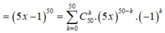
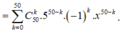Xét số hạng chứa  x 3 thì 50 - k = 3 => k = 47.

=> Hệ số của số hạng chứa  x 3  là: .

Ta có:

\(A_n^2 + 24C_n^1 = \frac{{n!}}{{\left( {n - 2} \right)!}} + 24.\frac{{n!}}{{1!\left( {n - 1} \right)!}} = n(n - 1) + 24n\)

\( \Leftrightarrow {n^2} + 23n = 140 \Leftrightarrow \left[ \begin{array}{l}n = 5\\n =  - 28\;(L)\end{array} \right.\)

Thay \(a = 2x,b =  - 1\) trong công thức khai triển của \({(a + b)^5}\), ta được:

\(\begin{array}{l}{(2x - 1)^5} = {\left( {2x} \right)^5} + 5.{\left( {2x} \right)^4}.( - 1) + 10.{\left( {2x} \right)^3}.{( - 1)^2}\\ + 10.{\left( {2x} \right)^2}.{( - 1)^3} + 5.(2x).{( - 1)^4} + {( - 1)^5}\\ = 32{x^5} - 80{x^4} + 80{x^3} - 40{x^2} + 10x - 1\end{array}\)

Đáp án D

Ta có:  ( x − 2 x 2 ) 21 = ∑ k = 0 21 C 21 k . x k . ( − 2 x 2 ) 21 − k = ∑ k = 0 21 C 21 k . x k − 2 ( 21 − k ) ( − 2 ) 21 − k

Số hạng không chứa x ó k – 2(21 – k) = 0 ó k = 14

Số cần tìm là C 21 14 ( − 2 ) 21 − 14 = C 21 7 ( − 2 ) 7   (theo tính chất C n k = C n n − k )