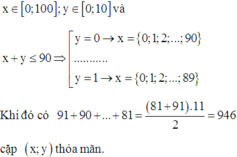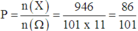Trong mặt phẳng Oxy, cho hình chữ nhật OMNP với M(0;1;0) ,N(100;10) và P(100;0). Gọi S là tập hợp tất cả các điểm A(x;y) với x , y ∈ ℤ nằm bên trong (kể cả trên cạnh) của OMNP . Lấy ngẫu nhiên một điểm A(x;y). Xác suất để x + y ≤ 90 bằng
A. 845 1111
B. 473 500
C. 169 200
D. 86 101